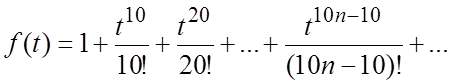
Вторая теорема разложения. Приложения операционного исчисления

Вторая теорема разложения. Пусть изображение   является дробно-рациональной функцией 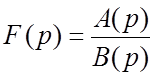от p: ,  и  - взаимно простые многочлены от p и  - полюсы этой функции (простые или кратные). Тогда оригинал, соответствующий изображению , определяется формулой

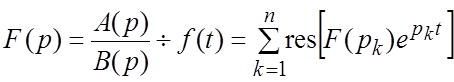                                  .                               (2.3)

 Замечание 1. Напомним, что в случае простого корня  вычет удобно искать по формуле

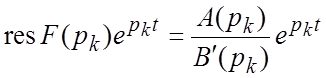                                 .                                         (2.4)

Если - полюс кратности , вычет ищут по формуле

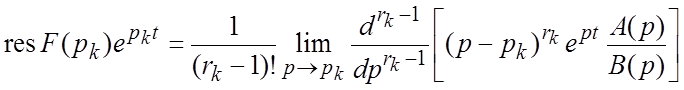            .                     (2.5)

          Замечание 2. Для каждой пары комплексных сопряженных корней  соответствующие им вычеты тоже числа комплексные сопряженные, и поэтому их сумма равна удвоенной действительной их части:

                     

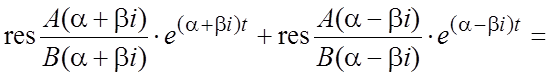
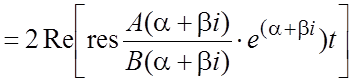                                     .                                         (2.6)

          Замечание 3. В том случае, когда кратность корней знаменателя выше второй, производные произведения двух функций удобно искать по формуле Лейбница:

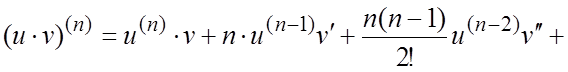
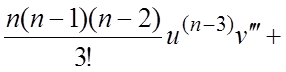
 .                                                                                           (2.7)

          Пример 2. Найти оригинал по данному изображению:

                                    .

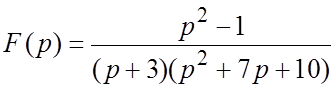          Решение. Здесь ;  ; . Корни знаменателя простые : ; ; . Оригинал определим с использованием формулы (2.4). Предварительно составим вспомогательную таблицу:

			- 4
			4
			1

Взяв алгебраическую сумму парных произведений членов двух последних столбцов таблицы, получим       .

Для сопоставления двух методов решим этот же пример при помощи разложения рациональной дроби на простейшие:

                                  .

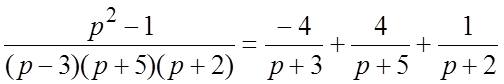Окончательно получим:

                                           .

          Пример 3. Найти оригинал по изображению .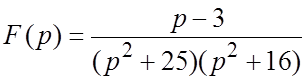

          Решение. Корни знаменателя : ; . Составляем вспомогательную таблицу, учитывая замечание 2:

С использованием формулы (2.6) отсюда найдем:

.

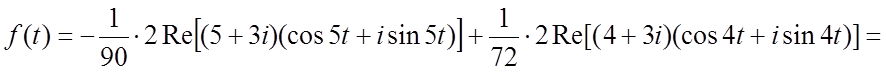
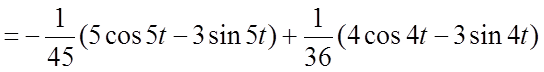          Пример 4. Найти оригинал для .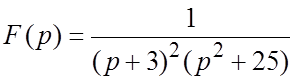

          Решение. Для знаменателя  корень  кратности ; корни - простые. Определение оригинала проведем по формуле (2.3), для чего следует найти вычеты функции  в полюсах :

.

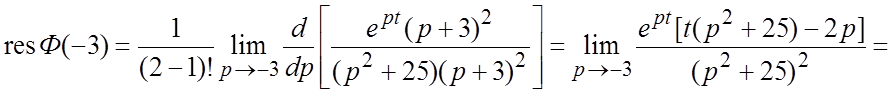
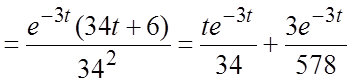Для определения  и  используем замечание 2:

.

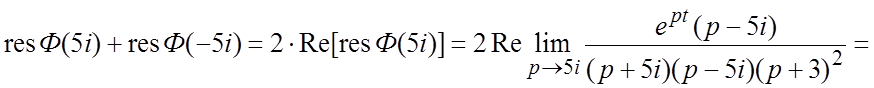
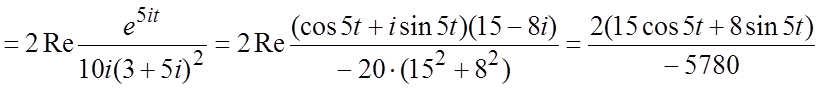Окончательно, по формуле (2.3) получим значение оригинала:

.

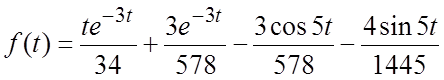          Пример 5. Найти оригинал для изображения .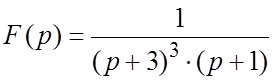

          Решение. Корни знаменателя  :  (кратность );  - простой. Найдем вычеты функции :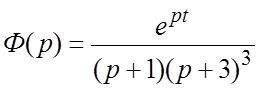

. 

.

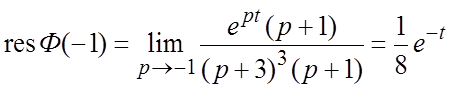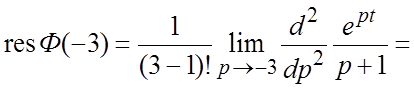
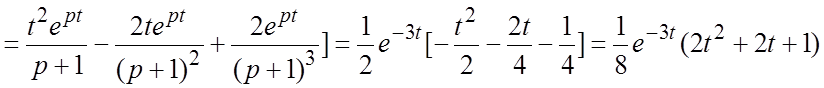Следовательно,  .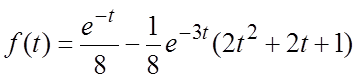

17.3.    Приложения операционного исчисления

17.3.1. Решение задачи Коши для обыкновенных дифференциальных

            уравнений с постоянными коэффициентами

          Задача Коши: найти решение уравнения

                                        ,                                      (3.1)

где , удовлетворяющее начальным данным: , , ..., . Задача Коши имеет решение в операторной форме:

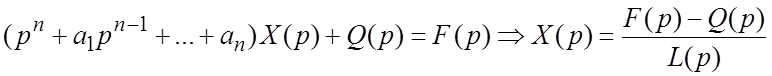             ,       (3.2)

где - изображение искомого решения, ,   -  характеристическое уравнение, - некоторый многочлен, коэффициенты которого зависят от  начальных данных . Находя по  оригинал , тем самым найдем функцию - решение задачи Коши (3.1).

          Пример 1. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: ; .

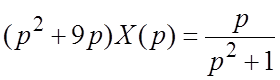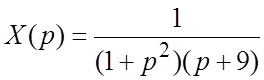          Решение. Перепишем данное уравнение в операционной форме: , откуда получим: . Чтобы перейти от изображения  к оригиналу , применим вторую теорему разложения. Корни знаменателя  простые: ; , . Составим вспомогательную таблицу:

	1	82
	1