Запишем решение задачи Коши:
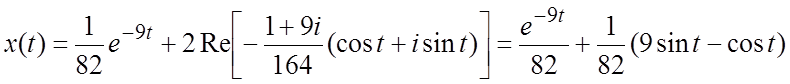 .
.
Пример 2. Найти частное решение
дифференциального уравнения ![]() , удовлетворяющее
начальным условиям:
, удовлетворяющее
начальным условиям: ![]()
![]() .
.
Решение. В операционной
форме имеем 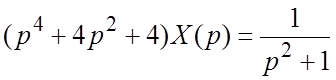 , откуда
, откуда 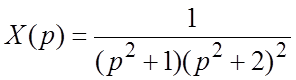 .
Для перехода от изображения к оригиналу применим вторую теорему разложения.
Корни знаменателя
.
Для перехода от изображения к оригиналу применим вторую теорему разложения.
Корни знаменателя ![]() :
: ![]() ,
, ![]() - (простые);
- (простые); ![]() ,
, ![]() - двукратные. На основании формул (2.3) и
(2.6) можно записать:
- двукратные. На основании формул (2.3) и
(2.6) можно записать: ![]()
![]() , где обозначено
, где обозначено ![]() . По формуле (2.4)
. По формуле (2.4) 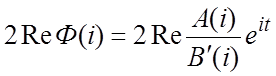 ,
где
,
где ![]() ;
; ![]() ;
; ![]()
![]() . Таким образом,
. Таким образом, 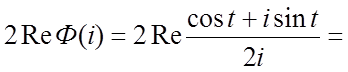
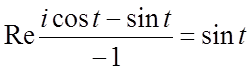 . Имеем далее,
. Имеем далее, ![]()
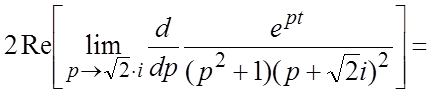
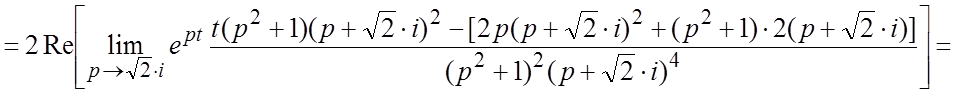
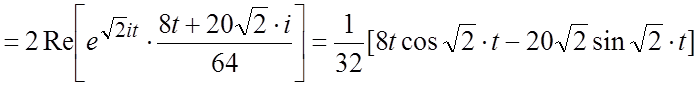 и,
следовательно,
и,
следовательно,
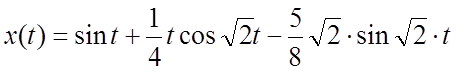 .Если
считать величины
.Если
считать величины ![]() произвольными постоянными, то найденное
решение будет общим решением уравнения (3.1).
произвольными постоянными, то найденное
решение будет общим решением уравнения (3.1).
Пример 3. Найти общее решение уравнения ![]() , а также частное решение его,
удовлетворяющее начальным условиям:
, а также частное решение его,
удовлетворяющее начальным условиям: ![]() ;
; ![]() .
.
Решение. Запишем исходное
дифференциальное уравнение в операционной форме, полагая, что ![]() - произвольные величины. Так как
- произвольные величины. Так как 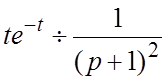 , то операционное уравнение примет вид:
, то операционное уравнение примет вид: ![]()
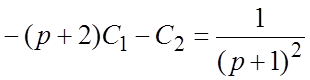 . Отсюда найдем
. Отсюда найдем 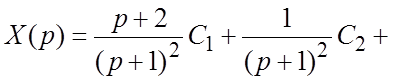
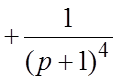 . Представив X(p) в виде
. Представив X(p) в виде 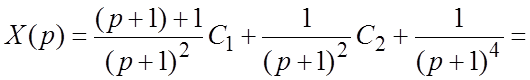
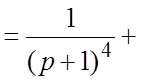
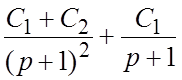 ; по таблице изображений находим решение:
; по таблице изображений находим решение: 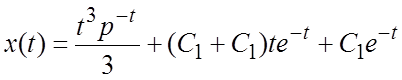 . Подставляя в него заданные начальные условия,
определяя произвольные постоянные
. Подставляя в него заданные начальные условия,
определяя произвольные постоянные ![]() , получим частное
решение:
, получим частное
решение: 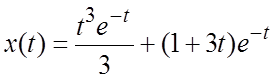 .
.
Пример 4. Проинтегрировать уравнение ![]() при нулевых начальных условиях, если
при нулевых начальных условиях, если
![]()
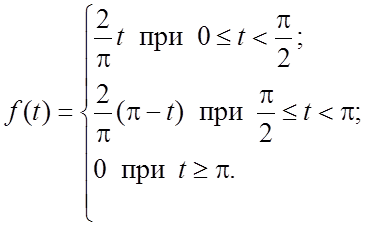
Решение. Запишем ![]() с
помощью единичной функции Хевисайда:
с
помощью единичной функции Хевисайда:
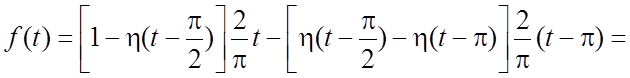
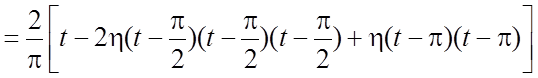 .
.
По теореме запаздывания (1.11) отсюда находим
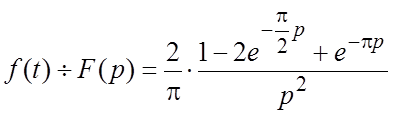 .
.
При нулевых начальных условиях приходим к определенному уравнению:
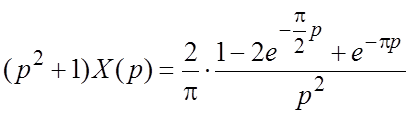 , из которого после несложных
преобразований находим:
, из которого после несложных
преобразований находим: 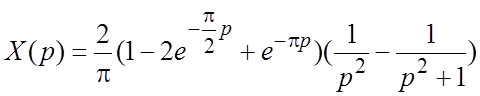 . Так как
. Так как 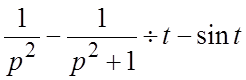 , то, снова применяя теорему запаздывания,
найдем
, то, снова применяя теорему запаздывания,
найдем
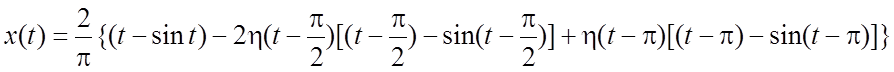 ,
,
или в обычной форме
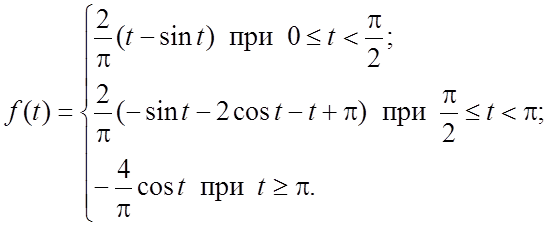
В некоторых случаях – опустим подробности – операционным методом удается решить линейное дифференциальное уравнение с переменными коэффициентами, являющимися некоторыми многочленами от t. Приведем пример.
Пример 5. Найти общее решение уравнения ![]() .
.
Решение. Пусть ![]() . Тогда
. Тогда ![]() ,
, ![]()
![]() ,
, 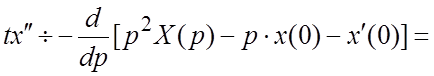
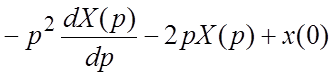 . Исходное уравнение принимает вид:
. Исходное уравнение принимает вид: 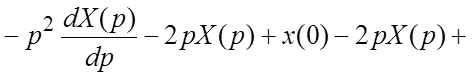
![]() или
или 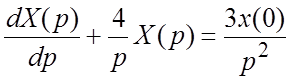 . Интегрируя это уравнение как линейное
неоднородное дифференциальное уравнение относительно
. Интегрируя это уравнение как линейное
неоднородное дифференциальное уравнение относительно ![]() ,
найдем
,
найдем 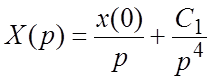 , откуда
, откуда 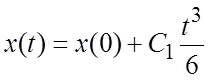 есть
решение исходного уравнения.
есть
решение исходного уравнения.
Приведем еще пример решения дифференциального уравнения с запаздывающим аргументом.
Пример 6. Решить уравнение ![]() ,
, ![]() .
.
Решение. Переходя к изображениям, получим 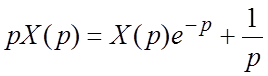 ,
,
откуда 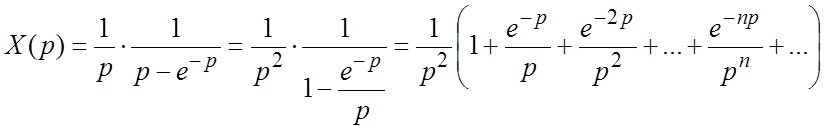 . Для
. Для ![]() получаем:
получаем: 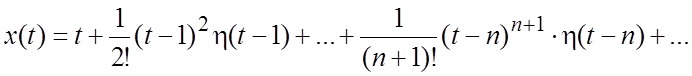 .
.
17.3.2. Интеграл Дюамеля. Решение систем линейных
дифференциальных уравнений операционным методом
1°. Интеграл Дюамеля. Пусть требуется решить линейное
неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка (3.1) при нулевых
начальных условиях. Допустим, что известно решение ![]() уравнения
(3.1) с правой частью, равной единице и нулевых начальных условиях. Тогда решение
уравнения
(3.1) с правой частью, равной единице и нулевых начальных условиях. Тогда решение
![]() уравнения (3.1) при нулевых начальных
условиях и произвольной правой частью
уравнения (3.1) при нулевых начальных
условиях и произвольной правой частью ![]() определяется
формулой Дюамеля (1.15):
определяется
формулой Дюамеля (1.15):
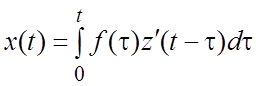 . (3.3)
. (3.3)
Пример 1. Решить уравнение 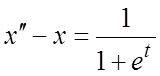 при нулевых начальных условиях.
при нулевых начальных условиях.
Решение. Решим вспомогательную
задачу: ![]() ,
, ![]() . Применяя
операционный метод, находим
. Применяя
операционный метод, находим 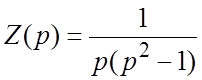 , откуда
, откуда 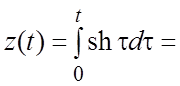
![]() . По формуле (3.3)
. По формуле (3.3) 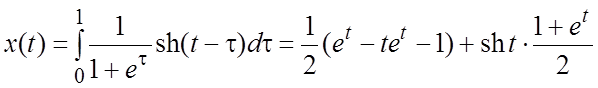 .
.
2. Системы линейных дифференциальных уравнений с постоянными коэффициентами. Решение системы линейных дифференциальных уравнений с постоянными коэффициентами операционным методом производится по той же схеме, что и решение одного дифференциального уравнения. Ввиду отсутствия принципиальных моментов, ограничимся лишь примером.
Пример 2. Операционным методом решить
систему дифференциальных уравнений 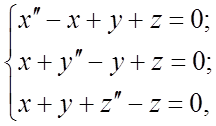 при начальных
условиях
при начальных
условиях ![]() ,
, ![]()
![]() .
.
Решение. Операционная система имеет вид
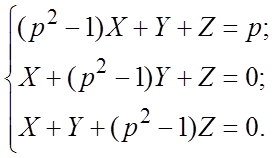
Ее решение получим с помощью определителей (по правилу Крамера):
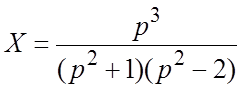 ;
;
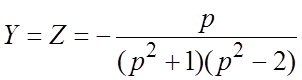 .
.
По второй теореме разложения находим оригиналы
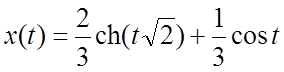 ;
; 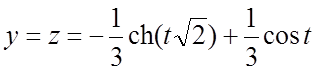 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.