Г Л А В А 12
12.1. ФУНКЦИОНАЛЬНЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ
Ряд
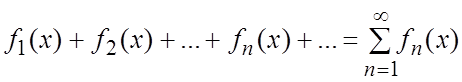 ,
(1.1)
,
(1.1)
членами которого
являются функции от x , определенные на
множестве D, называется функциональным рядом.
Если числовой ряд 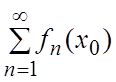 сходится, где
сходится, где ![]() , то
, то ![]() называется
точкой сходимости ряда (1.1). Множество всех точек сходимости ряда (1.1)
называется областью сходимости ряда (1.1). Если существует
называется
точкой сходимости ряда (1.1). Множество всех точек сходимости ряда (1.1)
называется областью сходимости ряда (1.1). Если существует 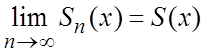 , где
, где ![]() ,
, ![]() , то говорят, что ряд (1.1) сходится на
множестве X к S(x). S(x)
называется суммой ряда (1.1). На языке “
, то говорят, что ряд (1.1) сходится на
множестве X к S(x). S(x)
называется суммой ряда (1.1). На языке “![]() ” это можно записать так:
” это можно записать так:
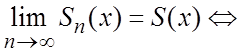
![]() .
.
Для нахождения области сходимости ряда (1.1) можно использовать эталонные ряды и достаточные признаки сходимости числовых рядов.
Пример. Найти область сходимости ряда 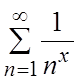 .
.
Ñ Данный ряд представляет собой обобщенный
гармонический ряд, который сходится при ![]() и
расходится при
и
расходится при ![]() . Областью сходимости ряда
является интервал
. Областью сходимости ряда
является интервал ![]() .#
.#
Пример. Найти область сходимости ряда 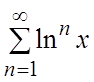 .
.
Ñ Данный ряд является геометрической
прогрессией, которая сходится, если ![]() .
. 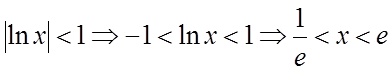 . Область сходимости ряда – интервал
. Область сходимости ряда – интервал 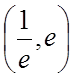 .#
.#
Пример. Найти область сходимости ряда
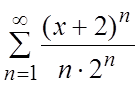 (a)
(a)
Ñ Для нахождения области сходимости данного ряда используем признак Даламбера, который применим лишь к рядам с положительными членами. Составим ряд из абсолютных величин членов данного ряда:
 (б)
(б)
и к нему
применим признак Даламбера (теорема 11.4). 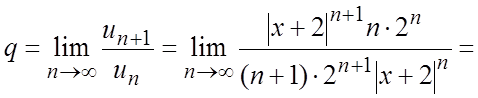
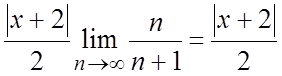 . Ряд (б) будет сходиться, если
. Ряд (б) будет сходиться, если 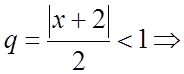
![]()
![]() .
Тогда ряд (а) будет сходиться, и притом абсолютно в интервале (-4, 0).
При
.
Тогда ряд (а) будет сходиться, и притом абсолютно в интервале (-4, 0).
При ![]() ряд (а) расходится, как не
удовлетворяющий необходимому признаку сходимости
ряд (а) расходится, как не
удовлетворяющий необходимому признаку сходимости ![]() (следствие из теоремы (11.1)). Если
(следствие из теоремы (11.1)). Если ![]() , то ответа о сходимости ряда признак
Даламбера не дает и при
, то ответа о сходимости ряда признак
Даламбера не дает и при ![]() и
и ![]() ряд нужно исследовать особо. При
ряд нужно исследовать особо. При ![]() из ряда (а) получим числовой ряд
из ряда (а) получим числовой ряд
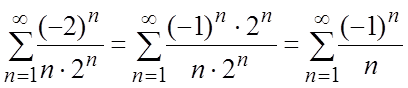 , который сходится
(ряд Лейбница) (см. задачу раздела (11.6)). При
, который сходится
(ряд Лейбница) (см. задачу раздела (11.6)). При ![]() из ряда
(а) получим
из ряда
(а) получим  - гармонический ряд, который
расходится (раздел 11.2). Итак, областью сходимости ряда (а) будет
промежуток [-4,0). #
- гармонический ряд, который
расходится (раздел 11.2). Итак, областью сходимости ряда (а) будет
промежуток [-4,0). #
Найти область сходимости следующих рядов.
1. 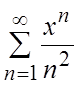 . 2.
. 2. 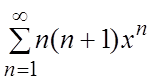 . 3.
. 3.
 . 4.
. 4. 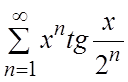 . 5.
. 5.
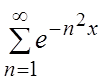 .
.
6. 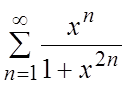 . 7.
. 7. 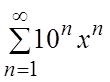 . 8.
. 8.
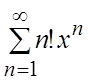 . 9.
. 9.  .
10.
.
10. 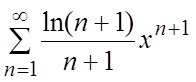 .
.
11. 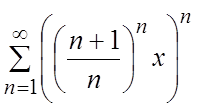 . 12.
. 12. 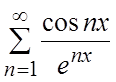 .
13.
.
13. 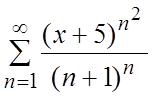 . 14.
. 14.  .
.
15.  . 16.
. 16. 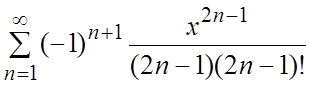 .
17.
.
17. 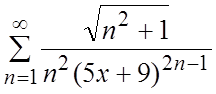 .
.
18. 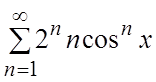 . 19.
. 19. 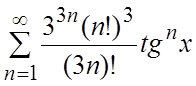 .
.
12.2. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
Сходящийся в некотором промежутке X
функциональный ряд 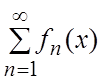 называется равномерно
сходящимся в этом промежутке к
называется равномерно
сходящимся в этом промежутке к ![]() , если
, если ![]()
![]() .
.
Теорема 1 (признак Вейерштрасса). Дан ряд (1.1). Если существует такой знакоположительный сходящийся числовой ряд
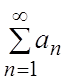 (2.1)
(2.1)
что ![]() , то ряд (1.1) сходится равномерно в
промежутке X.
, то ряд (1.1) сходится равномерно в
промежутке X.
Ряд (2.1) в этом случае называется мажорирующим рядом или мажорантой, а ряд (1.1) – мажорируемым сходящимся рядом (2.1).
Пример. Установить равномерную сходимость ряда 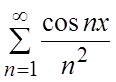 на любом отрезке.
на любом отрезке.
Ñ Рассмотрим ряд 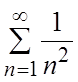 . Он
является знакоположительным, сходящимся (обобщенный гармонический,
. Он
является знакоположительным, сходящимся (обобщенный гармонический, ![]() ). Для
). Для ![]() справедливо
неравенство
справедливо
неравенство
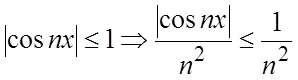 . Это
значит, что ряд
. Это
значит, что ряд 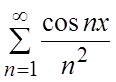 мажорируем на
мажорируем на ![]() , а значит сходится равномерно на любом
отрезке.#
, а значит сходится равномерно на любом
отрезке.#
Пример. Показать, что ряд 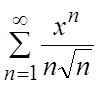 сходится
равномерно на [-1,1] .
сходится
равномерно на [-1,1] .
Ñ Для значений ![]() очевидно
очевидно
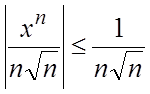 . Ряд
. Ряд 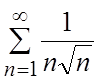 -
знакоположительный, сходящийся и, следовательно, по признаку Вейерштрасса ряд
-
знакоположительный, сходящийся и, следовательно, по признаку Вейерштрасса ряд 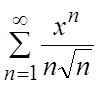 сходится равномерно на [-1, 1] .#
сходится равномерно на [-1, 1] .#
Пользуясь признаком Вейерштрасса, доказать равномерную сходимость следующих функциональных рядов в указанных промежутках.
20. 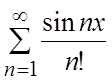 ,
, ![]() . 21.
. 21.  , [-3,
3]. 22.
, [-3,
3]. 22. 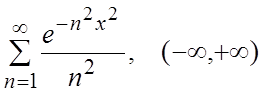 .
.
23. 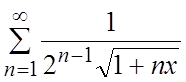 ,
, ![]() . 24.
. 24. 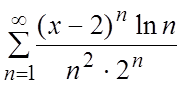 , [0, 4].
, [0, 4].
12.3. СВОЙСТВА РАВНОМЕРНО СХОДЯЩИХСЯ ФУНКЦИОНАЛЬНЫХ РЯДОВ
Теорема 2. Если члены ряда (1.1) – функции непрерывные в некотором
промежутке X и ряд сходится в этом промежутке
равномерно, то сумма его ![]() - функция также
непрерывная в X.
- функция также
непрерывная в X.
Теорема 3. Если члены ряда (1.1) –функции непрерывные в X и ряд сходится равномерно в X, то ряд можно почленно интегрировать на любом отрезке ![]() . Иначе говоря:
. Иначе говоря: 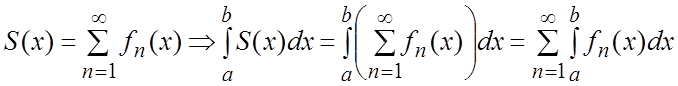 .
.
Теорема 4. Если 1) ряд (1.1) сходится в некотором промежутке X к S(x);
2) ![]() - функции непрерывные в X. 3) Ряд
- функции непрерывные в X. 3) Ряд 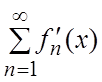 сходится равномерно в X, то ряд (1.1) можно почленно дифференцировать в каждой
точке промежутка X.
сходится равномерно в X, то ряд (1.1) можно почленно дифференцировать в каждой
точке промежутка X.
Т.е. 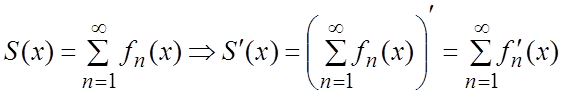 .
.
Пример. Исходя из соотношения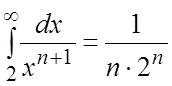 ,найти
сумму ряда
,найти
сумму ряда 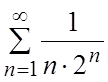 .
.
Ñ Т.к. члены ряда 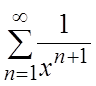 непрерывны
в
непрерывны
в ![]() и ряд сходится равномерно в этом
промежутке по признаку Вейерштрасса (теорема1):
и ряд сходится равномерно в этом
промежутке по признаку Вейерштрасса (теорема1): 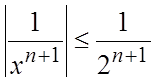 , т.е.
ряд
, т.е.
ряд 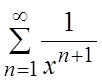 мажорируем сходящимся рядом
мажорируем сходящимся рядом 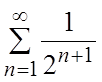 , то ряд
, то ряд 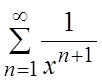 можно
почленно интегрировать на
можно
почленно интегрировать на ![]() , т.е. менять местами
символы
, т.е. менять местами
символы ![]() и
и ![]()
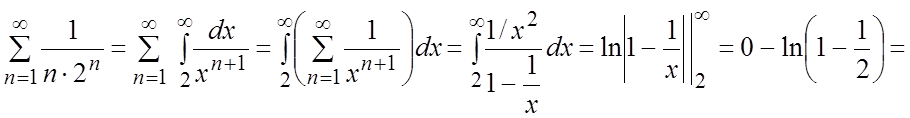
 .#
.#
12.4. СТЕПЕННЫЕ РЯДЫ. СВОЙСТВА СТЕПЕННЫХ РЯДОВ
Степенным рядом называется ряд вида
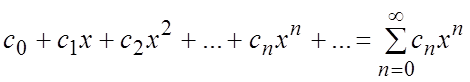 (4.1)
(4.1)
т.е. ряд,
членами которого являются степенные функции. Всякий степенной ряд (4.1)
сходится в интервале ![]() . R
называется радиусом сходимости ряда (4.1).
. R
называется радиусом сходимости ряда (4.1).
Если R = 0, то ряд (4.1) сходится только в точке x = 0. Если ![]() , то ряд (4.1) сходится
на всей числовой оси. Если
, то ряд (4.1) сходится
на всей числовой оси. Если ![]() , то интервалом
сходимости является конечный интервал с центром в точке x = 0 .
, то интервалом
сходимости является конечный интервал с центром в точке x = 0 .
Более общий вид степенного ряда:
![]() .
(4.2)
.
(4.2)
Интервал
сходимости этого ряда симметричен относительно точки ![]() :
:
![]() .
.
Теорема 5. На всяком отрезке ![]() ряд
(4.1) сходится равномерно.
ряд
(4.1) сходится равномерно.
Теорема 6. Степенной ряд (4.1) можно почленно интегрировать на
любом отрезке ![]() .
.
Т.о., если 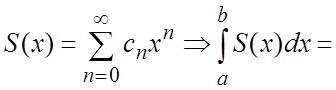

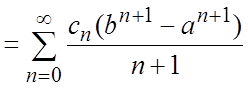 .
.
Теорема 7. Ряд (4.1) можно почленно дифференцировать в каждой точке x его интервала сходимости сколько угодно раз, при этом радиус сходимости ряда не меняется.
 .
.
Пример. Найти сумму ряда 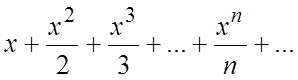
Ñ Обозначим сумму этого ряда через ![]() :
: 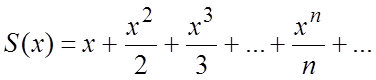
Интервал сходимости этого ряда (-1, 1). На основании теоремы 7 его можно почленно дифференцировать в каждой точке интервала (-1, 1):
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.