Раздел 7. Оптические и фотоэлектрические явления в полупроводниках.
Лекция 17. Введение. Макроскопическая электродинамика. Оптические константы. Вклад свободных носителей заряда в диэлектрическую проницаемость.
Шкала электромагнитных колебаний – от радиоволн до гамма-квантов, их взаимодействие с веществом. Макроскопическая электродинамика сплошных сред. Отклик среды на воздействие внешнего электрического поля. Приближение локального поля. Тензор диэлектрической проницаемости. Соотношения Крамерса-Кронига. Показатели преломления и поглощения. Вклад свободных носителей заряда в диэлектрическую проницаемость.
Введение. Шкала электромагнитных колебаний – от радиоволн до гамма-квантов. Оптические свойства полупроводников весьма важны для их практического применения в таких областях как фотоприёмники, светодиоды и лазеры. Оптический (видимый) диапазон электромагнитного излучения сравнительно узок – в длинах волн приблизительно от 0.38 до 0.8 микрометров. Так как в физике полупроводников энергетические характеристики часто обозначаются в электрон-вольтах (эВ), приведём коэффициент перевода длин волн в эВ - hn(эВ)=1.2398/l(мкм). Оптические свойствами полупроводников – это их взаимодействие с квантами электромагнитного излучения (фотонами) не только оптического диапазона, но и инфракрасного и ультрафиолетового диапазона. Весьма условно, этот диапазон можно рассматривать от СВЧ излучения (~10-4 эВ) до жёсткого ультрафиолета (~10 эВ).
Рассмотрим основные процессы, происходящие с фотонами при их взаимодействии с полупроводниками. При падении на поверхность полупроводника, часть излучения может отразиться. Прошедшее излучение преломляется, и может поглотиться. Наиболее важный с практической точки зрения механизм поглощения – поглощение либо с испусканием электрона в вакуум (внешний фотоэффект), либо с рождением внутри проводника электрона и дырки (внутренний фотоэффект). Прошедший свет может также рассеяться: как упруго (без потерь энергии) так и не упруго (с рождением либо поглощением квазичастицы в твёрдом теле – рассеяние Мадельштамма-Бриллюэна, комбинационное (Рамановское) рассеяние). Рожденные фотоном электрон и дырка, потеряв часть энергии (отдав кристаллической решётке) могут рекомбинировать с испусканием фотона с меньшей (чем у возбуждающего) энергией. Такой процесс называют фотолюминесценцией. Люминесценция может возникать также и при других типах возбуждения (создания неравновесных носителей заряда), наиболее важный из которых – электролюминесценция.
Если отклик среды пропорционален интенсивности возбуждающего света, такие процессы называют линейными. Мы практически не будем рассматривать нелинейные оптические процессы, такие как, например, генерация высоких гармоник, вынужденное комбинационное рассеяние света и другие.
Феноменологическое
описание. Макроскопическая электродинамика. Под влиянием внешнего
электрического поля среда поляризуется, при этом в полях с относительно малой
напряженностью ![]() связь между вектором
поляризации (единицы объема)
связь между вектором
поляризации (единицы объема) ![]() можно считать линейной [2.1
стр. 223, 1.9 § 77]:
можно считать линейной [2.1
стр. 223, 1.9 § 77]:
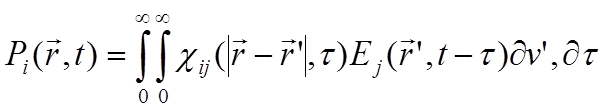 7.1
7.1
Тензор второго
ранга ![]() называется тензором электрической
восприимчивости.
называется тензором электрической
восприимчивости.
При этом
предполагается изотропность среды (связь между вектором поляризации в точке ![]() и напряженностью электрического поле в
точке
и напряженностью электрического поле в
точке ![]() зависит только от модуля расстояния
зависит только от модуля расстояния ![]() ). Согласно причинно-следственной связи,
вектор поляризации определяется напряженностью поля только в предшествующие
моменты времени.
). Согласно причинно-следственной связи,
вектор поляризации определяется напряженностью поля только в предшествующие
моменты времени.
Выражение 7.1 представляет собой свертку двух функций. Любое переменное поле может быть представлено (путём разложения в интеграл Фурье) как совокупность монохроматических волн. Легко показать, что свёртка функций в прямом пространстве преобразуется в произведение их Фурье компонент. Тогда, уравнение 7.1 сведется к уравнению:
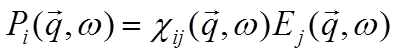 7.2
7.2
В большинстве
случаев, длина волны электромагнитного излучения много больше чем характерные
размеры в полупроводниковых кристаллах. Так, длина волны даже синего света
(4000 ангстрем в вакууме, либо приблизительно 1000 ангстрем в типичных
полупроводниках, с учётом коэффициента преломления) гораздо больше размера
элементарной ячейки (менее 5 ангстрем) или даже боровского радиуса волновой
функции электрона в водородоподобном атоме мелкой примеси (порядка 100
ангстрем). Тогда можно считать, что действие электрического поля носит
локальный характер, в предельном случае, можно считать, что зависимость тензора
электрической восприимчивости от модуля расстояния ![]() в
формуле 7.1 пропорциональна дельта-функции Дирака. Такое приближение называется
приближением локального поля. В этом случае можно
пренебречь пространственной дисперсией (зависимостью
в
формуле 7.1 пропорциональна дельта-функции Дирака. Такое приближение называется
приближением локального поля. В этом случае можно
пренебречь пространственной дисперсией (зависимостью ![]() от
волнового вектора
от
волнового вектора ![]() ). Формула 7.2 в этом приближении
сводится к следующему выражению:
). Формула 7.2 в этом приближении
сводится к следующему выражению:
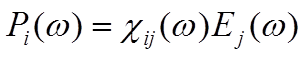 7.3
7.3
Связь между,
вектором индукции электрического поля в среде ![]() и
вектором напряженности электрического поля
и
вектором напряженности электрического поля ![]() заключается
в следующей формуле [1.5]:
заключается
в следующей формуле [1.5]:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.