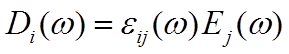 , где
, где 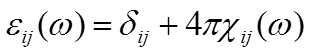 7.4
7.4
Тензор второго
ранга ![]() называется тензором диэлектрической
проницаемости,
называется тензором диэлектрической
проницаемости, ![]() - единичный тензор.
- единичный тензор.
В кристаллах с
низкой симметрией диэлектрическая проницаемость (и соответственно коэффициент
преломления и, соответственно фазовая скорость) может зависеть от направления
движения электромагнитной волны и от направления вектора её поляризации. В
таких кристаллах существует либо одна (одноосные кристаллы) либо две (двуосные
кристаллы) выделенных оптических оси. Фазовая скорость электромагнитных волн,
распространяющихся вдоль оптической оси, не зависит от направления вектора её
поляризации. Для других направлений, фазовая скорость зависит от поляризации –
так называемое явление двулучепреломления. В случае изотропной среды, (либо в
случае кристалла с высокой симметрией, например кубического) тензор
диэлектрической проницаемости имеет три одинаковых диагональных компонента и
его можно заменить на скалярную функцию диэлектрической проницаемости ![]() . Рассмотрим некоторые свойства этой
функции [1.9 стр. 394].
. Рассмотрим некоторые свойства этой
функции [1.9 стр. 394].
Для этого, воспользовавшись формулами 7.1, 7.4, и приближением локального поля запишем Фурье образ функции диэлектрической проницаемости в следующем виде:
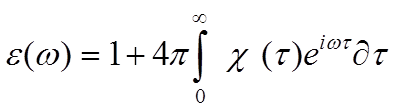 7.5
7.5
Вообще говоря,
функция ![]() комплексна, и её вещественную и мнимую
части обычно обозначают как:
комплексна, и её вещественную и мнимую
части обычно обозначают как:
![]() 7.6
7.6
Так как функция
![]() вещественна, то:
вещественна, то:
![]()
или ![]() а
а ![]() 7.7
7.7
Таким образом ![]() - чётная функция, а
- чётная функция, а ![]() - нечётная функция частоты, на верхней мнимой
полуоси (комплексная частота
- нечётная функция частоты, на верхней мнимой
полуоси (комплексная частота ![]() ) функция
) функция ![]() вещественна.
вещественна.
Функция ![]() конечна и стремится к нулю при
конечна и стремится к нулю при ![]() . При частотах, находящихся в верхней
комплексной полуплоскости, функция
. При частотах, находящихся в верхней
комплексной полуплоскости, функция ![]() экспоненциально
убывает. Значит, во всей верхней комплексной полуплоскости функция
экспоненциально
убывает. Значит, во всей верхней комплексной полуплоскости функция ![]() есть однозначная функция, не имеющая
никаких особых точек (полюсов), кроме простого полюса в точки
есть однозначная функция, не имеющая
никаких особых точек (полюсов), кроме простого полюса в точки ![]() для металлов. Отсутствие особых точек у
функции
для металлов. Отсутствие особых точек у
функции ![]() в верхней полуплоскости является следствием
принципа причинности [1.9 § 82]. Так как электромагнитные волны в средах
затухают, то мнимая часть функции
в верхней полуплоскости является следствием
принципа причинности [1.9 § 82]. Так как электромагнитные волны в средах
затухают, то мнимая часть функции ![]() положительна при
положительной вещественной части частоты
положительна при
положительной вещественной части частоты ![]() , и
отрицательна при отрицательной. Можно также доказать, что при
, и
отрицательна при отрицательной. Можно также доказать, что при ![]() по любому пути в верхней полуплоскости,
функция
по любому пути в верхней полуплоскости,
функция ![]() стремиться к единице. Физический смысл
этого заключается в том, что при частотах внешнего поля много больше всех
характерных частот в среде (скажем частота обращения электрона вокруг ядра
атома или плазменная частота в проводниках), среда не успевает реагировать на
изменения внешнего поля и электрическая восприимчивость стремиться к нулю
(более подробное рассмотрение смотри в [1.10 § 123]). Перечисленных свойств
функции
стремиться к единице. Физический смысл
этого заключается в том, что при частотах внешнего поля много больше всех
характерных частот в среде (скажем частота обращения электрона вокруг ядра
атома или плазменная частота в проводниках), среда не успевает реагировать на
изменения внешнего поля и электрическая восприимчивость стремиться к нулю
(более подробное рассмотрение смотри в [1.10 § 123]). Перечисленных свойств
функции ![]() достаточно, чтобы, используя теорию
функций комплексного переменного, вывести следующие соотношения:
достаточно, чтобы, используя теорию
функций комплексного переменного, вывести следующие соотношения:
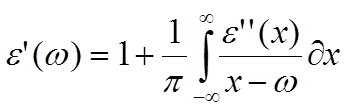
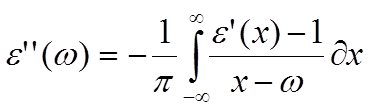 7.8
7.8
известные как соотношения Крамерса-Кронига. Интеграл от комплексного функции берётся в смысле главного значения. Что такое главное значение интеграла хорошо проиллюстрировано в книге [1.11 гл. 3 § 3].
Таким образом,
зная значение действительной части функции диэлектрической проницаемости ![]() во всем спектре, можно вычислить её мнимую
часть и наоборот. Так как большинство полупроводников немагнитные материалы, магнитная
проницаемость их близка к единице, и их показатели преломления и поглощения
определяются практически только диэлектрической проницаемостью. Соотношения,
подобные соотношениям Крамерса-Кронига, можно получить для реальной и мнимой
частей комплексного показателя преломления или для комплексного коэффициента
отражения [3.7]. Это весьма удобно для анализа экспериментально измеряемых
величин, чему и будет посвящён следующий раздел.
во всем спектре, можно вычислить её мнимую
часть и наоборот. Так как большинство полупроводников немагнитные материалы, магнитная
проницаемость их близка к единице, и их показатели преломления и поглощения
определяются практически только диэлектрической проницаемостью. Соотношения,
подобные соотношениям Крамерса-Кронига, можно получить для реальной и мнимой
частей комплексного показателя преломления или для комплексного коэффициента
отражения [3.7]. Это весьма удобно для анализа экспериментально измеряемых
величин, чему и будет посвящён следующий раздел.
Зная
комплексную диэлектрическую проницаемость (в предположениии, что материал у нас
не ферромагнетик, и магнитная проницаемость близка к единице) можно вычислить комплексный
показатель преломления ![]() . Обычно, комплексный
показатель преломления записывают в виде [3.12]:
. Обычно, комплексный
показатель преломления записывают в виде [3.12]:
![]() 7.9
7.9
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.