где n – показатель преломления, k – показатель
экстинкции, иногда используется и другая запись – 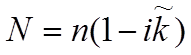 , тогда
, тогда ![]() называют
показатель поглощения. Эти оптические коэффициенты безразмерны, коэффициент
поглощения среды a,
имеет размерность обратной длины. Вычислим его из дисперсионного соотношения,
вытекающего из уравнений Максвелла:
называют
показатель поглощения. Эти оптические коэффициенты безразмерны, коэффициент
поглощения среды a,
имеет размерность обратной длины. Вычислим его из дисперсионного соотношения,
вытекающего из уравнений Максвелла: 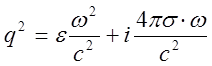 , где q- волновой вектор,
, где q- волновой вектор, ![]() ,
тогда, для случая малой проводимости
,
тогда, для случая малой проводимости 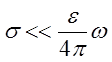 , с учётом того, что
интенсивность волны пропорциональна амплитуде в квадрате:
, с учётом того, что
интенсивность волны пропорциональна амплитуде в квадрате:
![]() 7.10
7.10
где l - длина волны в вакууме. Интенсивность
света в поглощающей среде зависит от расстояния как: 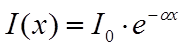 (закон
Бугера-Ламберта [3.13]).
(закон
Бугера-Ламберта [3.13]).
Вклад свободных носителей заряда в диэлектрическую проницаемость. Рассмотрим движение свободных зарядов под действием внешней электромагнитной волны. Пусть волна поляризована линейно, вектор поляризации направлен вдоль оси x. Так как скорости движения зарядов много меньше скорости света, пренебрежём вкладом магнитного поля в силу Лоренца. Если пренебречь рассеянием, то уравнение движения электрона запишется как:
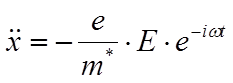
Решение ищем в
виде ![]() , тогда
, тогда 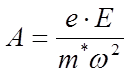 , и,
можно вычислить дипольный момент единицы объёма:
, и,
можно вычислить дипольный момент единицы объёма: 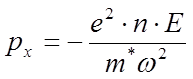 , а
электрическая восприимчивость
, а
электрическая восприимчивость 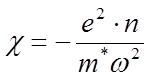 . Обратите внимание,
что заряд частицы входит в квадрате, и, значит, знак электрической
восприимчивости не зависит от знака заряда. Диэлектрическая проницаемость
электронного газа равна:
. Обратите внимание,
что заряд частицы входит в квадрате, и, значит, знак электрической
восприимчивости не зависит от знака заряда. Диэлектрическая проницаемость
электронного газа равна:
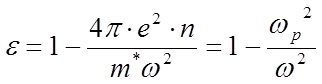 , где плазменная частота
, где плазменная частота 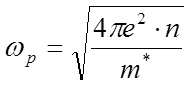 7.11
7.11
В области больших частот диэлектрическая проницаемость стремится к единице, электроны просто не успевают смещаться под воздействием поля такой высокой частоты, и не создают дипольного момента. Нарисуйте самостоятельно зависимость диэлектрической проницаемости электронного газа от частоты. При частотах меньше плазменной, она отрицательна, показатель преломления имеет комплексную часть. Такие волны сильно поглощаются средой. Оценим плазменную частоту для металлов и полупроводников. В металлах, концентрация свободных электронов достигает несколько единиц на 1022 см-3, и плазменная частота достигает значения порядка 1016 Герц (область частот видимого света и ультрафиолетового излучения). В полупроводниках (исключая сильнолегированные полупроводники), она на 3-4 порядка меньше (область частот акустических фононов, миллиметровый и субмиллиметровый диапазон электромагнитных волн).
Рассмотрим влияние рассеяния электронов (в приближении времени релаксации). Электрон ускоряется электрическим полем, но тормозится эффективной силой трения. В этом случае уравнение движения запишется как:
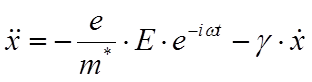
Найдём
константу g. В предыдущем разделе мы
рассматривали движение электрона в постоянном поле. Средняя дрейфовая скорость
его равна Vдр=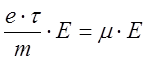 .
В этом случае сила со стороны электрического поля компенсируется эффективной
силой трения и среднее ускорение равно нулю. Тогда:
.
В этом случае сила со стороны электрического поля компенсируется эффективной
силой трения и среднее ускорение равно нулю. Тогда: 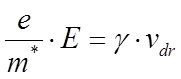 , и
, и 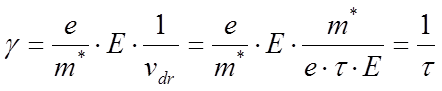 , а
, а 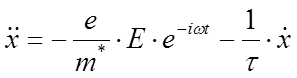
Решение также
ищем в виде ![]() , тогда
, тогда 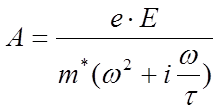 , и,
можно вычислить дипольный момент единицы объёма:
, и,
можно вычислить дипольный момент единицы объёма: 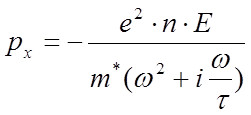 , а
электрическая восприимчивость
, а
электрическая восприимчивость 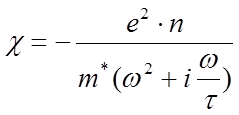 .
.
Диэлектрическая проницаемость электронного газа с учётом столкновений и рассеяния частиц равна:
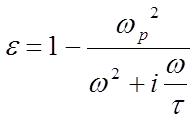 7.12
7.12
где плазменная
частота та же, что и в выражении 7.11. Можно вывести соотношение между
проводимостью и временем релаксации через плазменную частоту: 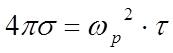 . Тогда:
. Тогда:
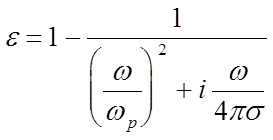
Выведем выражения для реальной и мнимой частей диэлектрической проницаемости:
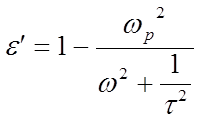
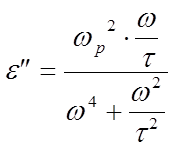 7.13
7.13
Попробуйте
самостоятельно построить график реальной и мнимой части диэлектрической
проницаемости в области всех частот для случая ![]() .
.
В приближении
времени релаксации также можно найти зависимость проводимости от частоты. 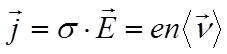
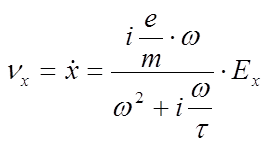 , отсюда
, отсюда 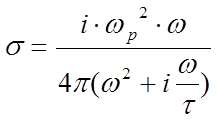 7.13a
7.13a
Отсюда, для металлов проводимость много меньше плазменной
частоты только при частотах много больших плазменной частоты, а при частотах
меньших ![]() проводимость вносит большой вклад в
поглощение.
проводимость вносит большой вклад в
поглощение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.