Оптические и фотоэлектрические явления в полупроводниках, страница 4

Лекция 18. Диэлектрическая проницаемость полупроводников. Экспериментальные методы исследования диэлектрической проницаемости полупроводников.

Вклад связанных носителей заряда в диэлектрическую проницаемость. Спектроскопия отражения и пропускания электромагнитных волн, эллипсометрия.

В лекции, посвящённой взаимодействию фононов с фотонами, мы уже рассматривали вклад связанных зарядов в диэлектрическую проницаемость среды. Рассмотрим гармонический осциллятор с затуханием, на который действует сила со стороны внешнего электрического поля E. Уравнение движения тогда будет:

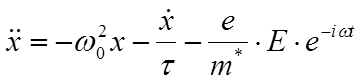
Решение снова ищем в виде , тогда 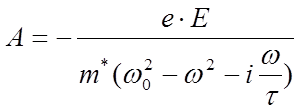, и, можно вычислить дипольный момент единицы объёма и вклад связанных зарядов в диэлектрическую проницаемость кристалла:

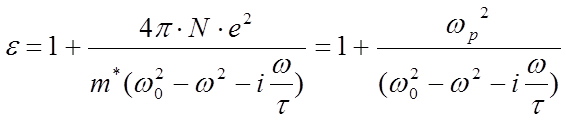                                       7.14

Попробуйте самостоятельно построить график реальной и мнимой части диэлектрической проницаемости в области всех частот для случая . Качественно постройте зависимость коэффициента поглощения от частоты электромагнитной волны для металлов (смотри предыдущую лекцию) и для полупроводников.

Экспериментальные методы исследования диэлектрической проницаемости полупроводников.

1) Отражение электромагнитных волн.

Наиболее простым методом определения оптических постоянных является измерение коэффициента отражения по интенсивности при нормальном падении электромагнитного излучения (рефлектрметрия). Измерения обычно проводят в вакууме, на рисунке 7.1 представлен типичный вакуумный рефлектометр [2.1].

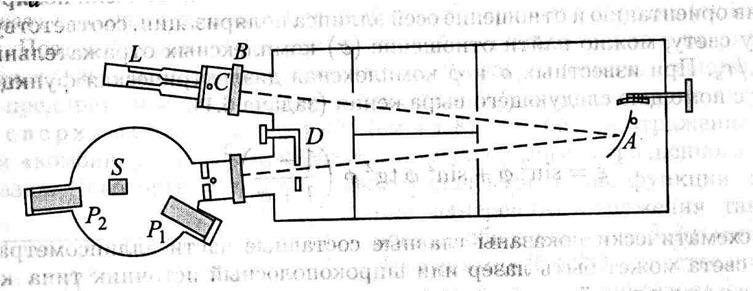
Рис. 7.1. Вакуумный рефлектометр: A – вогнутая дифракционная решётка, B и C – механизмы юстировки, D – держатель фильтра, L – лампа, S – держатель образца, P₁ и P₂ – приёмники излучения (фотоумножители).

Основные его части – широкополосный источник электромагнитного излучения (желательно от дальней инфракрасной (ИК) области до жёсткого ультрафиолета (УФ), дифракционные решётки (для получения узкой спектральной линии излучения) и приёмник отражённого излучения. Комплексный показатель отражения по амплитуде для нормального падения электромагнитной волны равен [1.5, 3.12]:

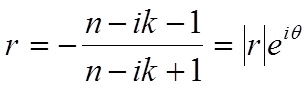                                   7.15

где n (действительный показатель преломления) – реальная, а k (показатель экстинкции) мнимая части комплексного показателя преломления. Напомним, что более часто употребляемый коэффициент поглощения (по интенсивности) a (с размерностью в обратных сантиметрах), выражается как , где l - длина волны в вакууме. Физический смысл комплексности показателя отражения состоит в том, что при отражении изменяется не только амплитуда, но и фаза волны (знак минус в выражении 7.9 иногда опускают, имея ввиду, что при отражении от оптически более плотной среды свет меняет фазу на противоположную). Энергетический (измеряемый) коэффициент отражения (то есть коэффициент отражения электромагнитной волны по интенсивности) составляет [1.5, 3.12]:

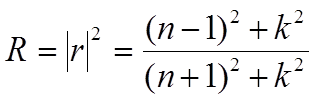                                 7.16

Выражения для R и фазового угла q (изменение фазы при отражении) также связаны соотношениями, вытекающими из анализа соотношений Крамерса-Кронига, интересующиеся могут найти их в справочнике 3.7 стр. 521. Зная R и q, можно, используя соответствующие выражения [3.7 стр. 516], вычислить n и k. Таким образом, зная в широком спектральном диапазоне коэффициент отражения электромагнитного излучения по интенсивности при нормальном падении, можно найти комплексный показатель преломления и, соответственно, спектральную зависимость функции диэлектрической проницаемости .

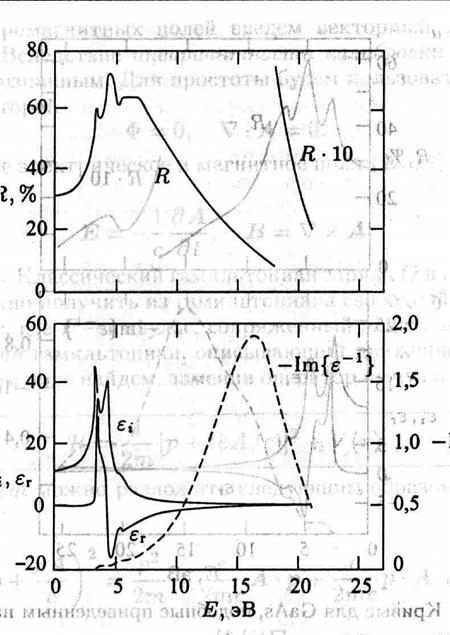
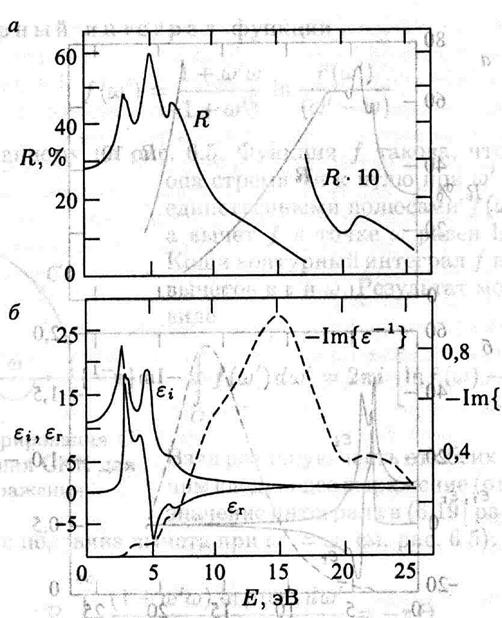
На рисунках 7.2 и 7.3 представлены зависимости коэффициента отражения по интенсивности от энергии падающего кванта, и, вычисленные  и  для кремния и арсенида галлия, соответственно. Измерения сделаны при комнатной температуре. Показана также функция энергетических потерь (мнимая часть от ). Пики в зависимости  связаны с переходами электронов из заполненных валентных зон в пустые зоны проводимости (при поглощении кванта электромагнитной волны).