Полупроводниковые структуры пониженной размерности

Раздел 9. Полупроводниковые структуры пониженной размерности.

Лекция 26. Квантовые ямы, проволоки и точки.

Граничные условия, квантование по импульсу и энергии. Плотность электронных состояний в полупроводниковых структурах пониженной размерности. Квантовые ямы, проволоки и точки.

Из курса квантовой механики вы знаете, что значение волновой функции частицы на границе с бесконечно высоким барьером равна нулю (так как волновая функция непрерывна, а в области бесконечно высокого барьера её амплитуда равна нулю). Значит, если зажать свободную частицу между двумя бесконечно высокими барьерами, проекция её импульса на ось z, перпендикулярную границам раздела барьер-яма будет не произвольной, а жёстко задана граничными условиями. Пусть расстояние между барьерами равно L. В нашем случае, в данном направлении, должно укладываться целое число полуволн: , в таком случае волновое число (и, соответственно, импульс) может принимать не любые, а дискретные значения . Энергетический спектр такой «заквантованной» частицы также претерпит изменения. Попробуем выяснить какие.

Объемный полупроводник.

Вспомним, как для объемного полупроводника зависит плотность состояний 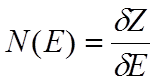 (количество состояний в интервале энергий от E до E+dE) от энергии электрона (или дырки) E. Для электрона с энергией близкой к минимуму энергии в зоне проводимости, зависимость энергии от волнового вектора квадратична:

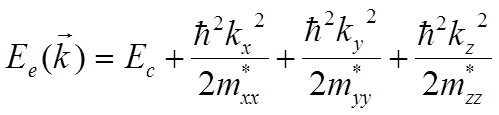   9.1

Тензор эффективной массы второго ранга m_ij здесь приведен к диагональному виду (для главных осей). Рассмотрим, для простоты, случай изотропной эффективной массы, тогда, уравнение 9.1 сведется к уравнению:

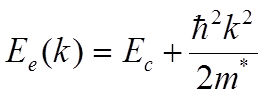                                         9.2

Так как, согласно запрету Паули, в одном квантовом состоянии может находиться не более 1 фермиона, значит, в состоянии с волновым вектором k_x, k_y, и k_z могут находиться 2 электрона (с учетом спина). В объеме полупроводника с размерами L_x, L_y, и L_z, для циклических граничных условий расстояние между соседними состояниями в обратном пространстве составляет 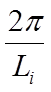. В обратном пространстве, занимающем объем 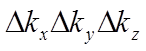 содержится  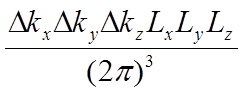состояний, различных по импульсу. Значит, в единичном объеме полупроводника содержится (с учетом спина) 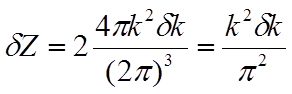 состояний с волновым вектором от k до k+dk.

 

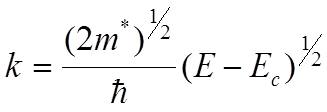
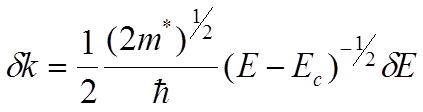
Таким образом, у дна зоны проводимости, в случае изотропной эффективной массы, плотность состояний составляет:

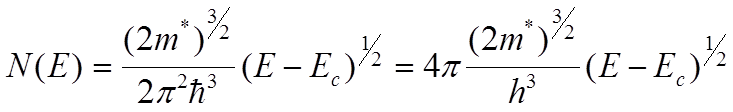            9.3

Одномерная квантовая яма (двумерный электронный газ).

Для электронов (либо дырок), находящихся в квантовой яме (двумерный электронный либо дырочный газ), движение по одной координате (скажем z) невозможно, k_z может принимать не любые значения, а только вполне определенные, определяющиеся из граничных условий. Движение «заквантовано» по координате z, и дисперсия энергии от волнового вектора в этом случае будет:

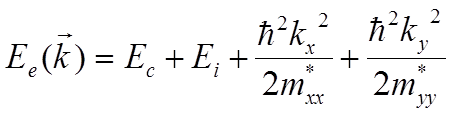
где E_i – уровни размерного квантования. Рассмотрим случай изотропной (в плоскости движения) массы, тогда в, двумерном газе (единичной площади), содержится 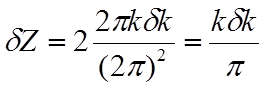 состояний с волновым вектором от k до k+dk. Плотность состояний для нулевого (самого нижнего E₀<E<E₁) уровня состояний будет:

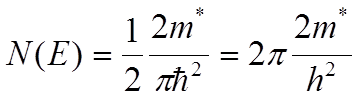                          9.4

Состояний электронов с энергией E_c<E<E₀ вообще нет, если энергия превышает первый уровень квантования, то плотность состояний увеличивается на величину N(E) из формулы 9.4, и так далее для более высоких уровней.

Квантовая проволока.

Рассмотрим электроны (либо дырки), движение которых ограничено по двум координатам (находящиеся в квантовой проволоке). Для проволоки единичной длины количество состояний с волновым вектором от k до k+dk равно: 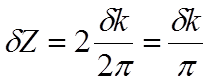. Тогда, плотность состояний для нулевого (самого нижнего E₀₀<E<E₀₁) уровня состояний будет:

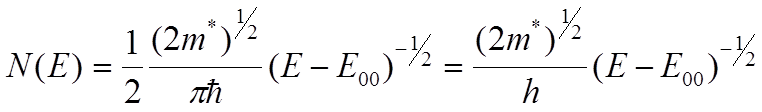            9.5

Так как электроны «заквантованы» по двум координатам, каждому уровню квантования соответствуют два квантовых числа, когда энергия превышает уровень квантования, возникает соответствующий всплеск плотности состояний.

Квантовая точка.

Рассмотрим случай, когда движение электронов (либо дырок) ограничено в некотором нуль-мерном объекте (то есть сам объект ограничен по всем трем координатам). Тогда, их импульс «заквантован» по всем трем координатам, а их энергия может принимать только строго дискретные значения. Классическая аналогия данному явлению – резонатор в электродинамике. В резонаторе незатухающими являются только волны с некоторыми частотами, удовлетворяющие граничным условиям. Можно также сказать, что квантовая точка это искусственно созданный атом, в котором набор энергетических уровней является дискретным (как, скажем в атоме водорода). Таким образом, энергетический спектр квантовой точки представляет собой набор дельта-функционных пиков.