Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 9

  Як приклад абсолютно стійкого методу традиційно розглядається неявний метод Ейлера, що має перший порядок апроксимації

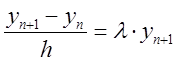               .                  (8.40)

З (8.40) випливає 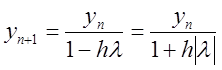, тобто  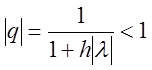завжди, при будь-яких  .

Умовна стійкість приводить до необхідності вибирати малі значення кроку , що є недоліком явного методу. Неявний метод, позбавлений даного обмеження, має інший досить істотний недолік, обумовлений необхідністю розв’язувати на кожному кроці алгебраїчне рівняння (або систему рівнянь, у загальному випадку нелінійних).

Запишемо різницеві рівняння (8.34) для задачі (8.37)

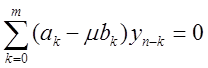 ,  ,(8.41)

де    - у загальному випадку комплексний параметр.

Характеристичне рівняння для (8.41) має вигляд

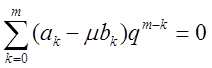  .                    (8.42)

При малих   корені (8.42) близькі до коренів (8.35).

Областю стійкості методу (8.34) називається множина точок комплексної площини , для яких метод, що застосований до рівняння спеціального вигляду (8.37), є стійким.

Для явного методу Ейлера умова стійкості  при комплексному   виглядає в такий спосіб: , тобто областю стійкості є коло одиничного радіуса, центр якого знаходиться в точці  комплексної площини.

Для неявного методу Ейлера умова 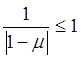  відповідає нерівності , тобто областю стійкості є зовнішність кола одиничного радіуса з центром у точці .

Різницевий метод називається стійким, якщо область його стійкості включає ліву півплощину  (або ). Варто звернути увагу на те, що рівняння (8.37) асимптотично стійке при . Отже,  стійкий різницевий метод є абсолютно стійким (тобто стійким при будь-яких ), якщо стійким є розв’язок вихідного диференціального рівняння.

З вищезазначеного видно, що неявний метод Ейлера має властивість стійкості, а явний метод – не має.

Розглянемо ще один неявний метод більш високого порядку апроксимації (другого):

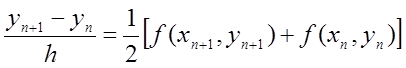               .     (8.43)

Цей метод виходить заміною інтеграла від правої частини (8.1) за формулою трапецій. Стосовно рівняння (8.37) метод (8.43) виглядає так: 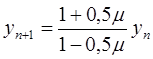      , тобто 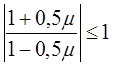, якщо . Отже, метод (8.43) належить до стійких методів.

Доведеними є такі положення:

  -серед методів (8.43) не існує явних стійких методів;

  -серед неявних лінійних багатокрокових методів немає стійких методів, що мають порядок точності вище другого.

  стійкі різницеві схеми досить ефективні при розв’язанні так званих жорстких систем рівнянь, оскільки ці методи не накладають обмежень на крок . Розглянемо докладніше це твердження.

8.2.4 Жорсткі диференціальні рівняння

Система звичайних диференціальних рівнянь

                                                              (8.44)

з незалежною від  матрицею  називається жорсткою, якщо ,   і відношення 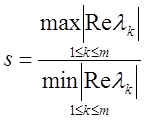  велике, де - власні числа матриці . Величина  називається числом жорсткості. Якщо матриця  залежить від , то і - залежать від  , тоді  вводиться змінне число жорсткості

                          

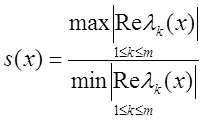
і оперують з величиною  на відрізку інтегрування.

Відмінною рисою жорстких систем є наявність у їхньому розв’язку як швидко, так і повільно спадних компонентів. При  розв’язок системи практично визначається повільно спадним компонентом, однак, якщо скористатися явними різницевими методами, то швидко спадна складова буде негативно впливати на стійкість, і в результаті весь розрахунок необхідно вести з малим кроком інтегрування. При використанні ж неявних методів обмеження на крок зняті, і його величину визначають з умови досягнення потрібної точності, не хвилюючись особливо за стійкість.

При розв’язанні жорстких систем диференціальних рівнянь добре зарекомендував себе метод Гіра, що належать до чисто неявних багатокрокових різницевих методів, загальна формула яких виглядає так:      ,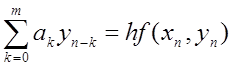

тобто розглядається частковий варіант методу (8.43), коли , а .

При  і  маємо , тобто неявний метод Ейлера. При  і  методи виглядають так:

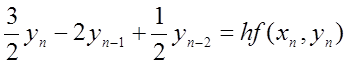                 ,            (8.45)

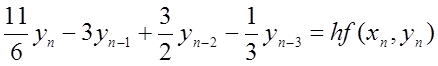              . (8.46)