Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 8

Виведемо групу явних багатокрокових формул. Для точок сітки введемо позначення  і припустимо, що нам відомі числові наближені значення  точного розв’язку  задачі (8.1)-(8.2).

З диференціального рівняння випливає

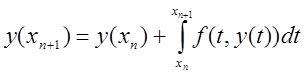.                     (8.29)

До правої частини (8.29) входить шуканий розв’язок . Але оскільки нам відомі його наближені значення , то ми маємо також і величини

,      (8.30)

а тому природно замінити функцію  в (8.29) інтерполяційним многочленом, що проходить через точки . Його можна виразити через скінченні різниці  вигляду  у такий спосіб:

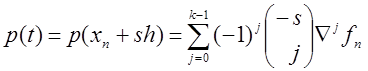                (8.31)

(інтерполяційна формула Ньютона). Тоді чисельний аналог (8.29) задається формулою 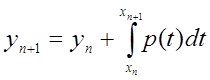, або після підстановки (8.31)

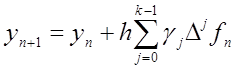,                       (8.32)

де коефіцієнти  задовольняють рівність

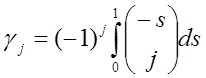.                           (8.33)

Числові значення цих коефіцієнтів наведені в таблиці 8.1.

Окремі випадки формули (8.32).

Для , виразивши різниці назад через , одержимо такі формули:

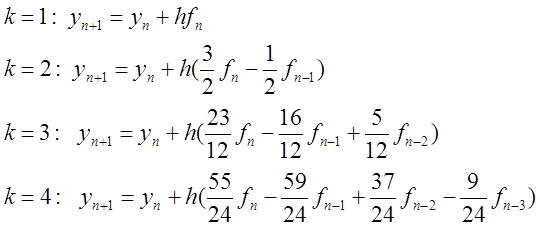
Зауваження. Для  ми маємо явний метод Ейлера.

Таблиця 8.1

	0  1    2       3        4          5         6           7               8
	1

Похибка апроксимації явного двокрокового методу Адамса має другий порядок.

Неявний двокроковий метод Адамса виглядає так:

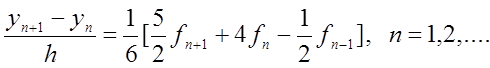
Похибка апроксимації має третій порядок .

8.2.3 Стійкість різницевих методів

Уведемо поняття стійкості різницевого методу. Для цього розглянемо різницеве рівняння багатокрокового методу

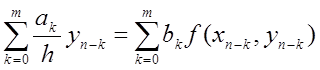 ,     .     (8.34)

Однорідне різницеве рівняння, що відповідає (8.34), має вигляд

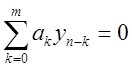 .                                     (8.35)

Вважають, що рівняння (8.35) є стійким за початковими даними, якщо існує постійна , що не залежить від , така, що при будь-яких початкових даних  здійснюється нерівність

                                ,  .

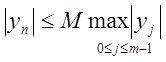Питання стійкості за початковими даними вирішується шляхом розгляду коренів так званого характеристичного рівняння, одержуваного з (8.35), якщо розв’язок цього рівняння шукати у вигляді  . Підставляючи таке  в (8.35) і скорочуючи на  , одержимо характеристичне рівняння для визначення

            .                (8.36)

Теорема 1 Для стійкості рівняння (8.35) за початковими даними необхідно і достатньо, щоб виконувалася так звана умова коренів: усі корені  характеристичного рівняння знаходилися всередині або на границі одиничного кола комплексної площини, причому на границі не повинно бути кратних коренів.

Теорема 2 Нехай ,  умова коренів виконана,  при , , і різницеве рівняння (8.34) апроксимує вихідне диференціальне рівняння (8.1). Тоді розв’язок різницевої задачі (8.34) збігається при  до розв’язку вихідної задачі (8.1).

Інакше кажучи, з апроксимації і стійкості за початковими даними випливає збіжність на обмеженому відрізку .

Сформульована умова стійкості, що базується на аналізі розміщення коренів характеристичного рівняння (8.36), є досить загальною. Конкретизуємо питання про стійкість різницевого рівняння стосовно до асимптотично стійких розв’язків рівняння (8.1). Нехай ,  , тобто

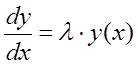                                    .                               (8.37)

Розв’язок цього рівняння асимптотично стійкий, тобто для будь-яких  справедлива оцінка

                                  .                           (8.38)

Логічно вимагати, щоб і різницеве рівняння давало розв’язок, що задовольняє властивість (8.38). Використовуючи явний метод Ейлера першого порядку апроксимації, одержимо різницевий аналог  (8.37)

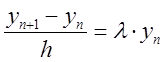                         ,         , (8.39)

або                                 ,  тобто   .

Оцінка (8.38) буде виконана для (8.39) лише за умови , оскільки тоді  . З  випливає обмеження на крок :  .

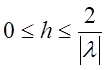Різницевий метод (8.34) називається абсолютно стійким, якщо стійкість має місце при будь-яких , й умовно стійким, якщо вона може бути забезпечена тільки введенням обмежень на крок .