Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 6

         Ейлера                         Рунге-Кутта  

Графіки наближених і точних розв’язків

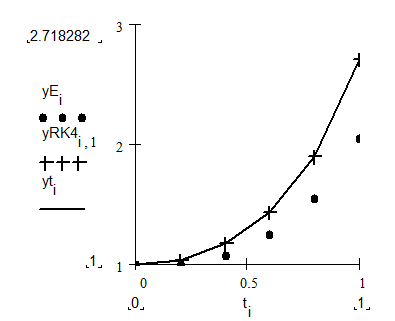
Обчислення похибки за правилом Рунге:

Обчислення наближених розв’язків із кроком h/2:

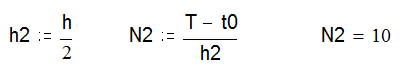
Обчислення похибок:   

.

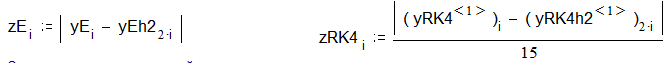
Приклад реалізації алгоритму методу Рунге-Кутта четвертого порядку з заданою точністю  на псевдокоді.

f(x,y):

 //повертає значення заданої похідної при заданих x та y

end

//BeginValue – початкові умови

//YF – відповідь – масив значень функції

//h – крок

//n – кількість точок розбиття

//eps – точність розрахунку

//Метод Рунге-Кутта 4-го порядку

SolveRungeKutt(BeginValue,YF,h,n,eps):

1  repeat

2   for j:=1 to 2 do

3   Y[j,1]:=BeginValue

4   for i:=1 to n do

5   x:=a+(i-1)*h

6   k1:=f(x,Y[j,i])

7  k2:=f((x+h/2),(Y[j,i]+h*k1/2))

8  k3:=f((x+h/2),(Y[j,i]+h*k2/2))

9   k4:=f((x+h),(Y[j,i]+h*k3))

10  Y[j,i+1]:=Y[j,i]+h*(k1+2*k2+2*k3+k4)/6

11   done

12  if j=1 then

13   h:=h/2

14   n:=round((b-a)/h)

15   fi

16   done

17   maxr:=0

18   for i:=1 to 10 do

19  r:=abs(Y[1][((n*i) div 20)+1]-

20   -Y[2][((n*i) div 10)+1])/15;

21   if r>maxr then

22   maxr:=r

23   fi

24   done

25   if maxr<eps then

26   for i:=1 to 10 do

27   YF[i]:=Y[2][((n*i) div 10)+1]

28   done

29   fi

30  until maxr<eps

end

8.2 Багатокрокові методи

8.2.1 Метод прогнозу і корекції

Підправивши  схему Ейлера  в середній точці одержимо схему прогнозу

                                 ,                            (8.20)

де наближене значення . Використовувати формулу (8.20) не можна через те, що схема прогнозу нестійка. З цієї причини  використовуємо  схему корекції 

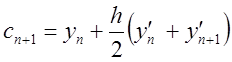                   (8.21)

Для оцінки похибки корекції розкладемо в ряд Тейлора в околі точки корекцію

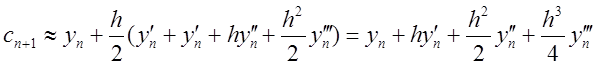
та саму функцію                    .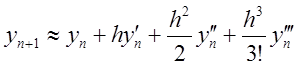

Віднявши ці два розкладання , отримаємо

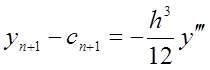                   .                       (8.22)

Для оцінки похибки прогнозу розкладемо в ряд Тейлора в околі точки прогноз

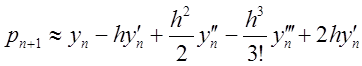 та саму функцію   

.

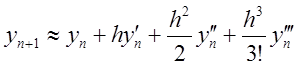Віднявши ці два розкладання , отримаємо похибку прогнозу

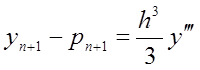             .                       (8.23)

З цих оцінок зрозуміло, що прогноз наближає розв’язок з недостачею, а корекція з надлишком. Отже, точне значення розв’язку лежить між прогнозом і корекцією. На будь-якому кроці можна оцінити точність розв’язку . Якщо задається її значення, то .

Віднімаючи рівності (8.23) та (8.22), маємо

                                         .

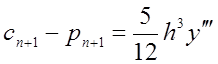Уточнюємо розв’язок, виходячи  з формули (8.22)

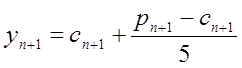                              .                    (8.24)

Відтак формула (8.24) завершує схему прогнозу і корекції. .

Приклад 1 Розв’язати задачу Коші для диференціального рівняння другого порядку:

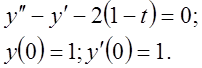
Розв’язання. 1 Введемо нові змінні :

U=y; V=. Тоді, обравши сітку , визначимо на ній сіткові функції :

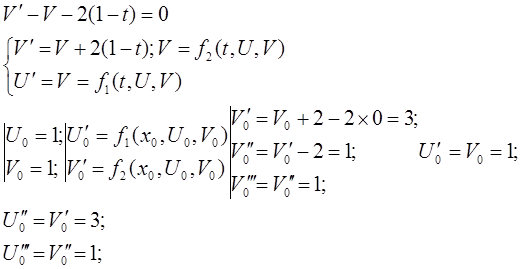
2         Знаходимо  і  () за допомогою розкладання в ряд Тейлора :

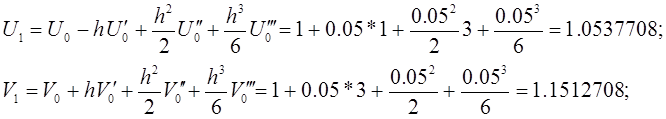       3         З диференціального рівняння знаходимо  і :

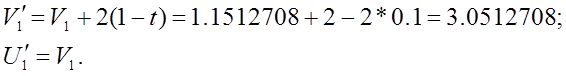
  Визначаємо прогноз розв’язку в точці

.

Тимчасово покладаючи U₂=P₂ ; , можна отримати

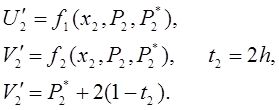
Обчислюємо корекцію 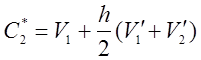. Тепер можна визначити V2

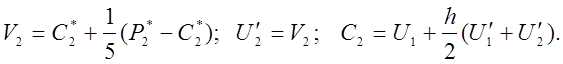
І нарешті на даному кроці уточнюємо розв’язок

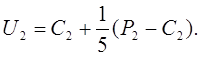
Похибка обчислення .

Приклад 2 Використовуючи метод прогнозу і корекції, реалізувати алгоритм розв’язку крайової задачі для звичайного диференціального рівняння з точністю  на псевдокоді.

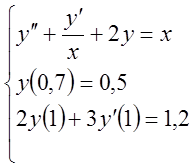
Розв’язання

Після заміни

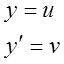
отримаємо (користуючись системою символічної математики Derive)

vo1:=-0.3-vo/(0.7)

vo2:=1-2*vo-(vo1*(0.7)-vo)/(0.7)^2

vo3:=-2*vo1-(vo2*(0.7)^3-2*(0.7)*(vo1*(0.7)-vo))/(0.7)^4

u1:=0.5+0.3*vo+vo1*(0.3)^2/2+vo2*(0.3)^3/6