Припустимо,
що початкова умова ![]() задана точно. При одержанні (8.5)
у формулі Тейлора був відкинутий член, що містить
задана точно. При одержанні (8.5)
у формулі Тейлора був відкинутий член, що містить ![]() .
.
На
першому кроці, при обчисленні ![]() , отримана похибка
, отримана похибка ![]() , яка називається локальною похибкою, або
похибкою на кроці.
, яка називається локальною похибкою, або
похибкою на кроці.
На
другому кроці ![]() обчислюється за формулою
обчислюється за формулою ![]() . Величина
. Величина ![]() ,
знайдена раніше, визначена наближено. Тому сумарна похибка на другому кроці
,
знайдена раніше, визначена наближено. Тому сумарна похибка на другому кроці ![]() буде викликана не тільки заміною
інтегральної кривої на відрізку
буде викликана не тільки заміною
інтегральної кривої на відрізку ![]() дотичною до неї, але і
помилкою, допущеною на першому кроці.
дотичною до неї, але і
помилкою, допущеною на першому кроці.
Аналогічно
сумарна похибка n-го кроку залежить не тільки від заміни інтегральної
кривої на відрізку ![]() дотичною, але і від помилок,
допущених при обчисленні
дотичною, але і від помилок,
допущених при обчисленні ![]() (рис. 8.2). У випадку,
коли початкова умова задана неточно, сумарна похибка на будь-якому кроці буде
залежати і від похибки початкової умови (8.2).
(рис. 8.2). У випадку,
коли початкова умова задана неточно, сумарна похибка на будь-якому кроці буде
залежати і від похибки початкової умови (8.2).
Розглянемо
похибку наближеного розв’язку ![]() , знайденого методом
Ейлера (рис. 8.2).
, знайденого методом
Ейлера (рис. 8.2).
Припустимо, що функція f(x, у) з (8.1) неперервна і має неперервні перші похідні в області зміни своїх аргументів. Віднімаючи (8.5) з (8.4) , одержимо
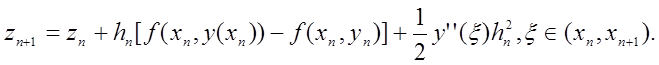 Використовуючи
формулу Тейлора, з урахуванням того, що
Використовуючи
формулу Тейлора, з урахуванням того, що ![]() ,
одержуємо
,
одержуємо
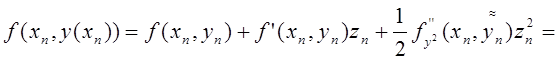
 .
.
Звідси
![]() .
.
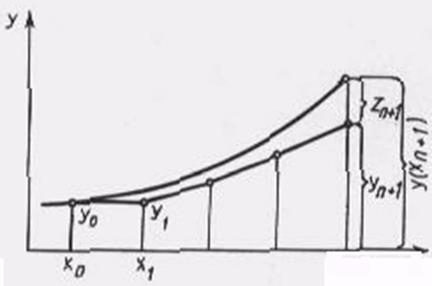
Рис. – 8.2
Отже, з точністю до величин більш високого порядку малості,
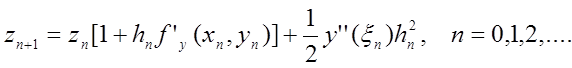
Таким чином,
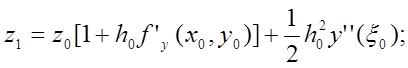
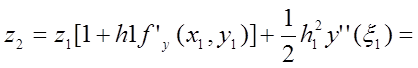
![]()
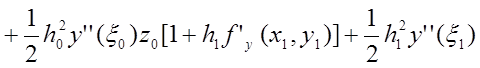 .
.
Аналогічно
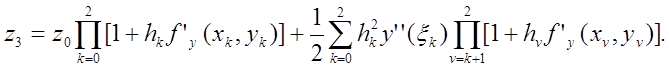 Продовжуючи цей процес,
одержимо
Продовжуючи цей процес,
одержимо
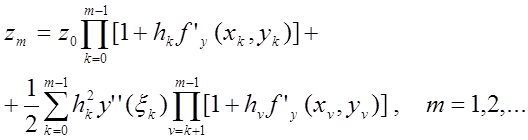 (8.6)
(8.6)
Таким
чином, похибка ![]() на довільному кроці m
виражається через похибку
на довільному кроці m
виражається через похибку ![]() .
.
При
малих ![]() має місце така оцінка:
має місце така оцінка:
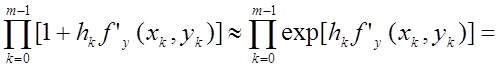
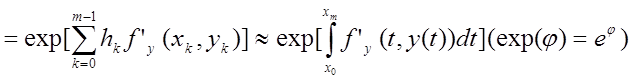 .
.
Аналогічно
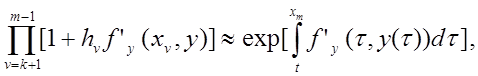
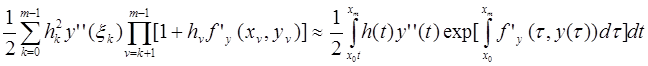 .
.
Тут h(t) – кусково-лінійна функція, значення якої
в кожному вузлі ![]() дорівнює
дорівнює ![]() .
.
Підставляючи ці вирази у формулу (8.6), одержимо оцінку похибки на довільному кроці m:
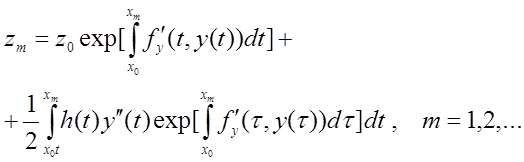 (8.7)
(8.7)
Вона
складається з двох доданків, перший з яких обумовлений похибкою ![]() початкових даних. Якщо вони точні,
початкових даних. Якщо вони точні, ![]() =0, що і будемо припускати надалі.
=0, що і будемо припускати надалі.
Поява другого доданка пов'язана з відкиданням у рівності (8.5) залишкового члена формули Тейлора. Оцінимо цей доданок зверху.
Припустимо,
що на відрізку ![]()
![]() , |
, |![]() , |
, |![]() .
.
Тоді
![]()
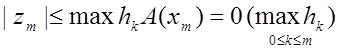 , де (8.8)
, де (8.8)
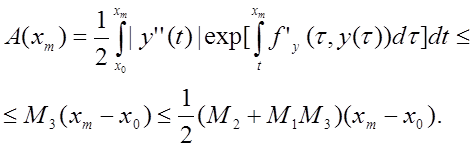
З нерівності (8.8) випливає твердження.
Якщо
f(x,y) неперервна й обмежена в системі зі своїми першими похідними в
області зміни своїх аргументів, то наближений розв’язок задачі (8.1) – (8.2),
знайдений методом Ейлера, при ![]() збігається до точного
розв’язку рівномірно на обмеженому відрізку
збігається до точного
розв’язку рівномірно на обмеженому відрізку ![]() із
сумарною похибкою
із
сумарною похибкою ![]() .
.
Отже, метод Ейлера має перший порядок точності.
8.1.2 Схеми Рунге-Кутта другого порядку
Невисокий
ступінь точності методу Ейлера визначається перш за все тим, що залишковий член
формули (8.4) ![]() . Зажадаємо, щоб
. Зажадаємо, щоб ![]() . За формулою Тейлора
. За формулою Тейлора
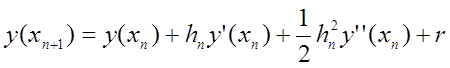 ,
,
де залишковий член
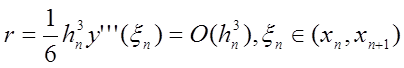 . (8.9)
. (8.9)
Рівність
(8.9) справедлива, якщо у'’’(x) обмежена на ![]() . З
(8.1) випливає
. З
(8.1) випливає
![]() .
.
Тут
треба обчислювати частинні похідні функції f(x,y), що з причин,
зазначених раніше, небажано. Щоб уникнути диференціювання, замінимо ![]() виразом
виразом
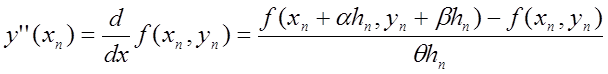 ,
,
де ![]() - деякі параметри. Тоді, якщо у формулі
(8.9) відкинути залишок r , одержимо
- деякі параметри. Тоді, якщо у формулі
(8.9) відкинути залишок r , одержимо
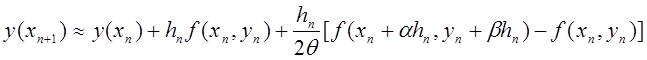 ,
,
або ![]() , (8.10)
, (8.10)
де ![]() ;
; ![]() .
.
Параметри
![]() виберемо так, щоб розкладання точного
розв’язку
виберемо так, щоб розкладання точного
розв’язку ![]() задачі (8.1)- (8.2) у вузлі
задачі (8.1)- (8.2) у вузлі ![]() і його наближення
і його наближення ![]() ,
що обчислюється за формулою (8.10), у ряди за степенями
,
що обчислюється за формулою (8.10), у ряди за степенями ![]() , збігалися з точністю до нескінченно малої
найбільш високого порядку щодо
, збігалися з точністю до нескінченно малої
найбільш високого порядку щодо ![]() .
.
Для одержання точного розв’язку використовуємо формулу (8.9)
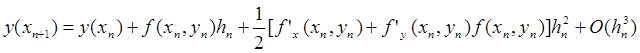 ,
,
аналогічно для наближеного розв’язку
![]() +
+
![]()
![]() .
.
Припускаючи,
що ![]() , і порівнюючи члени при однакових степенях
, і порівнюючи члени при однакових степенях ![]() , одержимо
, одержимо ![]()
Для
визначення чотирьох невідомих параметрів маємо три рівняння. Виразимо ![]() через інші параметри:
через інші параметри: 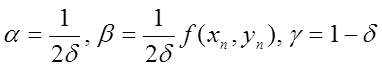 .
.
Підставляючи ці значення у (8.10), одержимо однопараметричне сімейство двочленних схем Рунге-Кутта:
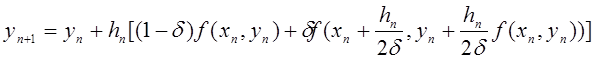 (8.11)
(8.11)
Відзначимо,
що вибрати параметр ![]() так, щоб збігалися коефіцієнти у
формулі Тейлора при
так, щоб збігалися коефіцієнти у
формулі Тейлора при ![]() , неможливо.
, неможливо.
Формула
(8.11) завдяки своїй досить великій точності широко використовується в
чисельних розрахунках, при цьому найчастіше беруть або ![]() , або
, або ![]() .
.
Підставляючи
в (8.11) ![]() , одержимо розрахункову формулу
, одержимо розрахункову формулу
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.