Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 4

,      (8.12)

відому як формулу вдосконаленого методу Ейлера.

При використанні даного методу спочатку за формулою (8.5) обчислюємо наближене значення розв’язку при . Після цього в знайденій точці визначаємо нахил інтегральної кривої: , а потім знаходимо значення

.

Покладаючи в (8.11)  =0,5, одержимо

  (8.13)

При використанні формули (8.13) спочатку обчислюється за методом Ейлера наближене значення , потім  нахил інтегральної кривої в новій точці (рис. 8.4) Після цього визначається уточнене значення

.              (8.14)

Розрахункова схема (8.13) або (8.14) називається методом Ейлера-Коші, або обчислювальним правилом типу предиктор-коректор.

Для схеми (8.14) можна довести, що якщо f(x,y) неперервна й обмежена разом зі своїми другими похідними, то розв’язок, отриманий за схемою (8.11) при будь-якому  і при , рівномірно збігається до точного розв’язку із сумарною похибкою . Отже, схема (8.11) має другий порядок точності.

8.1.3 Схеми Рунге-Кутта четвертого порядку

Методом Рунге-Кутта можна будувати схеми різного порядку точності.

Так схема ламаних Ейлера (8.5) є схемою Рунне-Kyттa першого порядку точності. Найбільш уживані схеми четвертого порядку точності. Наведемо без виведення найчастіше використовувані з них:

,

   ,

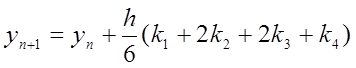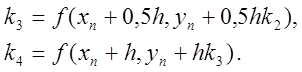                                      (8.15)

Відзначимо, що формули більш високого порядку точності практично не вживаються через громіздкість, що зростає значно швидше, ніж точність формули.

Схеми Рунге-Кутта мають ряд переваг:

1) мають досить високий ступінь точності (за винятком схеми ламаних);

2) є явними, тобто значення  обчислюється за раніше знайденими значеннями;

3) допускають використання змінного кроку, що дає можливість зменшити його там, де функція швидко змінюється, і збільшити в іншому випадку;

4) є легко застосовними, тому що для початку розрахунку досить вибрати сітку  і задати значення .

Зазначені властивості схем досить корисні при розрахунках на ЕОМ.

Оцінки похибок різних схем Рунге-Кутта пов'язані з максимумами модулів відповідних похідних функції  досить складними формулами типу (8.8). У зв'язку з цим при розв’язанні конкретної задачі виникає питання, якою з формул Рунге-Кутта доцільно користуватися і як обирати крок сітки.

Якщо f(х,у) неперервна й обмежена разом зі своїми четвертими похідними, то гарні результати дає схема четвертого порядку (8.15). Якщо права частина рівняння (8.1) не має зазначених похідних, то граничний порядок точності схеми (8.15) не може бути реалізований. Тоді доцільно користуватися схемами меншого порядку точності, що дорівнює порядкові наявних похідних, наприклад для двічі неперервно диференційованої функції f(x,y) —схемами (8.12) і (8.1З).

Крок сітки варто вибирати настільки малим, щоб забезпечити необхідну точність розрахунку. З огляду на складність виразів залишкових членів (типу 8.8) апріорною (від лат. a priori — з попередніх) оцінкою точності для вибору кроку при практичних розрахунках не користуються, а заміняють її, наприклад, розрахунками зі згущенням сітки і дають апостеріорну (від лат. a posteriori - з наступного) оцінку точності.

Зауваження. Якщо функція f(x,y) досить гладка, але швидко змінюється на , схеми Рунге-Кутта як низького, так і високого порядку точності вимагають неприйнятно малого кроку для отримання задовільного результату. Для таких задач використовуються спеціальні методи, орієнтовані на даний вузький клас задач.

Одним із найбільш простих, широко застосовуваних і досить ефективних методів оцінки похибки й уточнення отриманих результатів у наближених обчисленнях з використанням сіток є правило Рунге.

Нехай маємо наближену формулу 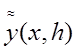 для обчислення величини у(х) за значеннями на рівномірній сітці  і залишковий член цієї формули має такий вигляд:

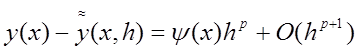.            (8.16)