Чисельне розв’язання звичайних диференціальних рівнянь. Різницева апроксимація диференціальних рівнянь однокроковими методами, страница 2

Вивчення різницевих апроксимацій проводиться спочатку локально, тобто в будь-якому фіксованому вузлі сітки.

При розв’язуванні диференціальних рівнянь чисельним методом основним є питання про збіжність. Стосовно до різницевих методів традиційно більш уживане поняття збіжності при . Позначимо за  значення сіткової функції, що відповідає значенню точного розв’язку диференціального рівняння 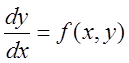 у вузлі -  ( є  наближеними значеннями ). Збіжність при  означає таке. Фіксуємо точку  і будуємо сукупність сіток  таким чином, що  і  (при цьому ). Тоді вважають, що чисельний метод збігається в точці , якщо  при , . Метод збігається на відрізку , якщо він збігається в кожній точці . Вважають, що метод має -й порядок точності, якщо можна знайти таке число , що  при .

Уведемо далі поняття нев'язки, або похибки, апроксимації різницевого рівняння, що заміняє задане диференціальне рівняння, на розв’язку вихідного рівняння, тобто нев'язка  являє собою результат підстановки точного розв’язку рівняння   у різницеве рівняння. Наприклад, рівняння 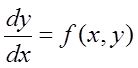 можна замінити таким найпростішим різницевим рівнянням

,    .

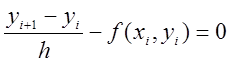Тоді нев'язка визначиться як  .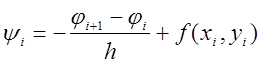

Наближений розв’язок не збігається з , тому нев'язка  в -ій точці не дорівнює нулеві.

Чисельний метод апроксимує вихідне диференціальне рівняння, якщо  при , і має -й порядок точності, якщо .

Доведено, що порядок точності чисельного методу розв’язання диференціального рівняння збігається з порядком апроксимації при досить загальних припущеннях.

8.1.1 Метод Ейлера

Ознайомлення з чисельними методами розв’язання звичайних диференціальних рівнянь першого порядку почнемо з вивчення методу Ейлера для задачі Коші

,                               (8.1)

.                               (8.2)

Відзначимо, що на практиці цей метод використовується рідко через невисоку точність, однак він є найпростішим з чисельних методів і на його прикладі зручно пояснити їх суть, способи побудови і дослідження.

Для розв’язання задачі потрібно знайти наближені значення  точного розв’язку  рівняння (8.1). Уведемо позначення . Припустимо, що розв’язок  задачі (8.1) — (8.2) у вузлі  відомий. Знайдемо розв’язок у наступному вузлі  . Використовуючи формулу Тейлора, одержимо

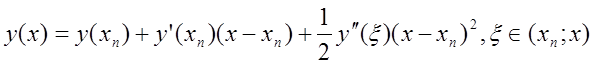 (8.3)

Відзначимо, що похідну , що стоїть у правій частині, можна знайти, диференціюючи рівняння (8.1).

Підставимо у формулі (8.3) , тоді

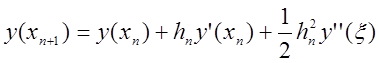.          (8.4)

Припускаючи, що  на відрізку  обмежена, маємо 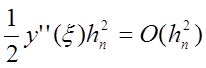. Однак використовувати формулу (8.4) незручно з таких міркувань:

1) вираз  може виявитися громіздким; 2) якщо права частина рівняння (8.1) відома лише приблизно, що часто має місце при розв’язанні технічних задач, знаходити її похідні небажано.

Якщо  має q-і неперервні похідні по сукупності аргументів, то в розкладанні (8.3) можна враховувати значення членів аж до

Відкидаючи в (8.4) величини другого порядку малості при  в порівнянні з кроком сітки , одержуємо формулу для обчислення наближеного значення  у вузлі  З огляду на те, що , виводимо розрахункову формулу методу Ейлера

.                    (8.5)

Для чисельного розрахунку за формулою (8.5) досить знати . Потім, використовуючи (8.5), можна послідовно знайти значення розв’язку  відповідно в точках

                                                 Рис. – 8.1

Геометрична інтерпретація методу Ейлера показана на рис. 8.1, де зображена множина інтегральних кривих рівняння (8.1). Використання тільки першого члена формули Тейлора рівносильне заміні інтегральної кривої на відрізку [] дотичною до неї в точці (). На кожному кроці заново визначається дотична, і, отже, траєкторія буде ламаною лінією. Тому метод Ейлера називають також методом ламаних.

При визначенні наближеного розв’язку задачі надзвичайно важлива оцінка похибки використовуваного методу. Розглянемо таку оцінку для методу Ейлера.