Оцінка функціональної ефективності системи керування, що навчається, страница 9

P_m(<d_m )=Ф()-Ф(-)=2Ф() – 1.

Аналогічно, якщо позначити  d_l = x_l – (x_m+d_m), то отримаємо

P_l (| X_l -x_l | < d_l) = 2Ф () – 1.

Звідки

P_l (X_l < d_l ) =  [1- (2Ф () – 1)] =1-Ф() .

Тоді

h_m,l = = .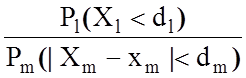

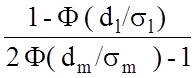Таким чином, коефіцієнт парного перетину  h_m,l  залежить від міжцентрової відстані класів    і  , яка дорівнює  d(x_mx_l) = d_m+ d_l ,  і середньоквадратичних відхилень реалізацій класів від своїх центрів розсіювання, що і стверджувалося. При цьому збільшення  d_l  при незмінних  d_m, s_m  і  s_l  призводить до зменшення коефіцієнту  h_m,l, а збільшення  s_l   при незмінних   d_m , d_l   і  s_m – до його збільшення. Перетин класів відсутній, якщо  P_l(X_l < d_l) = 0, тобто  Ф() =1,  і для нормально розподіленої випадкової величини  X_l  все розсіювання вкладається на інтервалі  | X_l  - 3s | < d_l . Так само  P_m(<d_m)0, оскільки  Ф()0.5  при  d_m >0  і  s_m < .  Значення  h_m,l =1  може бути тільки при збіганні центрів розсіювання  x_m  і  x_l  за умови  d_m=d_l . При цьому екстремальне значення функції розподілу дорівнює 2/3 за умови  s_m = s_l  .

Т в е р д ж е н н я 3.8.2.  Збільшення парного коефіцієнта перетину класів розпізнавання при  сталих дисперсіях  s_m і  s_l  призводить до зменшення повної вірогідності класифікатора.

Д о в е д е н н я.  Розглянемо залежність коефіцієнта  h_m,l  від межи  d_m  області класу  X. Аналіз виразу (3.8.3) показує, що зменшення  d_m   призводить до зменшення аргументу, а отже і значення функції  Ф(d_m/s_m), що зменшує знаменник виразу. З іншого боку, збільшується аргумент і значення функції  Ф(d_l/s_l),  що призводить так само до зменшення чисельника виразу (3.8.3). Таким чином, тенденція зміни значення коефіцієнту  h _{m, l} ,  залежно від зміни межи області класу  X, є невизначеною і потребує аналізу точнісних характеристик. Для з’ясування впливу параметра  d_m  на достовірність розпізнавання розглянемо таку інтерпретацію коефіцієнта парного перетину (3.8.3). Тут, у чисельнику, ймовірність  P_l (X_l < d_m)  є не що інше, як помилка другого роду: b=p{X[x_m – d_m, x_m + d_m] ¤ x_l  X }, а ймовірність у знаменнику –  це перша достовірність: D₁ = p{X_m  [x_m - d_m, x_m+d_m] ¤ X_m  X}.

Таким чином,

                                                          h _{m, l} =  .                                                 (3.8.4)

Із виразу (3.8.4) витікає, що при  b = const  зменшення перетину класів призводить до збільшення першої достовірності розпізнавання випадкової величини  X_m. Для узагальнення розглянемо коефіцієнт  h _{m ,l}  як відношення     повної ймовірності  Р_f    неправильного розпізнавання  X_m  до повної ймовірності  Р_t  правильного розпізнавання  X_m :

h_m,l =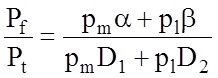 ,                                  (3.8.5)

де        - імовірності появи випадкових величин   X_m ;

            – імовірності появи випадкових величин  X_l .

У випадку відсутності апріорної інформації доцільно за принципом недостатньої обґрунтованості гіпотез прийняти  == 0.5. Тоді

h_{m, l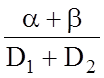} = .                                           (3.8.6)

З урахуванням зв’язку між точнісними характеристиками однієї групи подій: ,  , можна стверджувати, що збільшення коефіцієнту перетину класів розпізнавання призводить до збільшення повної ймовірності неправильного розпізнавання реалізацій образу, тобто до зменшення першої та другої вірогідностей. Таким чином, показано, що запропонований коефіцієнт перетину класів розпізнавання дозволяє оцінювати асимптотичну точність розпізнавання образів і визначити при збільшенні алфавіту класів розпізнавання її критичну потужність. Підхід до корекції екстремальних точнісних характеристик навчання за МФСВ при збільшенні алфавіту класів розпізнавання буде розглянуто в підрозділі 6.5.

3.9. Оцінка функціональної ефективності СК з урахуванням

експлуатаційних витрат на її навчання