Оцінка функціональної ефективності системи керування, що навчається, страница 8

3.8. Оцінка точнісних характеристик навчання СК з відкритим алфавітом класів розпізнавання

Одним із важливих показників СК, що навчається, є асимптотична повна достовірність розпізнавання  , яка визначається функціональною ефективністю навчання системи та характеризує потенційні точнісні характеристики побудованого в процесі навчання вирішального правила. Поява нових класів, що може призводити як до збільшення ступеня перетину класів, так і до зменшення їх середньої міжкласової відстані, обумовлює зниження асимптотичної ймовірності правильного прийняття рішень. Проаналізуємо вплив потужності відкритого алфавіту класів розпізнавання на асимптотичні (екстремальні) точнісні характеристики процесу навчання СК при незмінному словнику ознак розпізнавання.

Нехай {X|m=,...}^-відкритий алфавіт класів розпізнавання, який поповнюється в процесі функціонування СК новими класами. У бінарному просторі ознак  W_Б  задано навчальну матрицю  і множину еталонних векторів  }. Розіб’ємо множину    на пари сусідніх векторів  = < x_m, x_l >  за умови мінімальної кодової відстані між ними, яку позначимо через  d(x_mx_l), , lm, де  x_l - еталонний вектор класу  X, найближчого до класу  X. Для визначення факторів, що впливають на зменшення вірогідності  D_1,m  при збільшенні потужності алфавіту  ,  розглянемо характеристики розбиття простору  W_Б, які безпосередньо впливають на точнісні характеристики. Введемо парний коефіцієнт перетину для класу  X, який у геометричній інтерпретації має вигляд:

h_m,l=V_m () / V_m  ,                                        (3.8.1)

де      V_m() - область перетину класу    з класом  ,  lm;

          V_m - обсяг контейнера класу  ;

і множинний коефіцієнт перетину для класу  X:

                           q_m,1..r=V_m(X  X) / V_m ,  lm ,                        (3.8.2)

де      r - кількість перетинів для класу X,  r < M–1.

При прийнятті гіпотези нечіткої компактності реалізацій образів обчислення характеристик (3.8.1) і (3.8.2) у рамках МФСВ не викликає ускладнень, оскільки контейнери класів розпізнавання будуються в радіальному базисі і їх геометричні параметри визначаються в процесі навчання системи за ітераційною процедурою пошуку максимуму інформаційного критерію. Розглянемо твердження, які встановлюють вплив потужності абетки    на достовірність рішень, що приймаються.

Т в е р д ж е н н я 3.8.1.  Нехай у бінарному просторі  W_Б ознак розпізнавання потужності  N  здійснюється за МФСВ нечітке розбиття на  M  класів, в якому задано множину вершин еталонних векторів  , і відома кодова відстань між центрами сусідніх класів  d(x_mx_l), то парний коефіцієнт  h _{m, l}  перетину класу    з класом    залежить як від міжцентрової відстані класів розпізнавання, так і від середньоквадратичних відхилень реалізацій класів, що перетинаються.

Д о в е д е н н я.  Нехай випадковий вектор-реалізація образу має нормальний розподіл. Для наглядності розглянемо дві системи двох випадкових величин  (N=2)  з  функціями щільності розподілу  f(x₁, x₂)  і  f _l (x₁, x₂),  центрами розсіювання яких є відповідно вершини векторів  x_m  і  x_l. Відомо, що перерізи поверхні розподілу двох випадкових величин, проведені паралельно функції щільності, аналогічні кривим нормального розподілу для однієї випадкової величини. На рис.3.10  наведено такий переріз поверхней розподілу для функцій  f( x₁, x₂)  і  f _l (x₁, x₂)  з дисперсіями    і   (<),  який проходить через їх центри розсіювання.

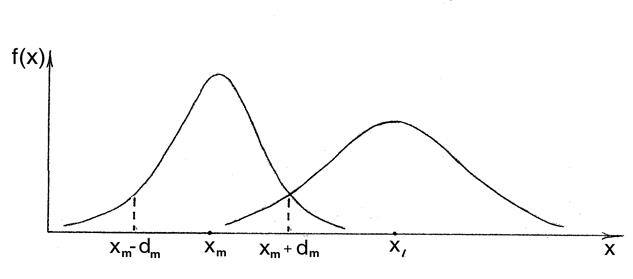
Рис.  3.10.  Переріз функції щільності ймовірностей для класів    і

Парний коефіцієнт перетину класів (3.8.1) у ймовірнісній інтерпретації, згідно з рис. 3.10, має вигляд:

h _{m ,l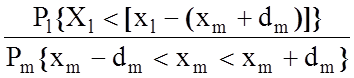} = ,                           (3.8.3)

оскільки областями класів    і є симетричні інтервали  [x_m-d_m;  x_m +d_m]  і   [x_l - (x_l – (x_m+ d_m));  x_l+ (x_l – (x_m+ d_m))]  відповідно.

З урахуванням властивості функції нормального розподілу:          Ф(-x)=1-Ф(x),  отримаємо