Оцінка функціональної ефективності системи керування, що навчається, страница 5

          n_min - мінімальний обсяг репрезентативної навчальної вибірки.

Після підстановки відповідних позначень (3.5.1) в (3.2.2) отримаємо робочу модифіковану формулу для обчислення в рамках МФСВ ентропійного інформаційного КФЕ навчання СК розпізнаванню реалізацій класу    

  

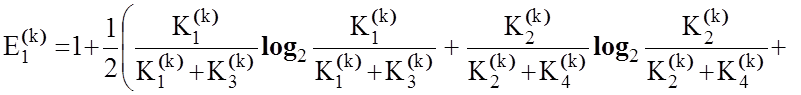
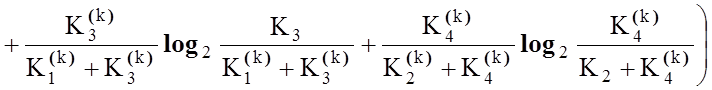     .        (3.5.2)

Опис структурної схеми алгоритму обчислення  критерію (3.5.2) за паралельним способом оброблення навчальної матриці в процесі побудови у радіальному базисі оптимального контейнера класу    наведено в додатку А. На рис. 3.6 показано проведені паралельно вертикальної поверхні  D₁0E (рис. 3.2)  перерізи тривимірної поверхні функції  E = f (D₁ , D₂ ).  

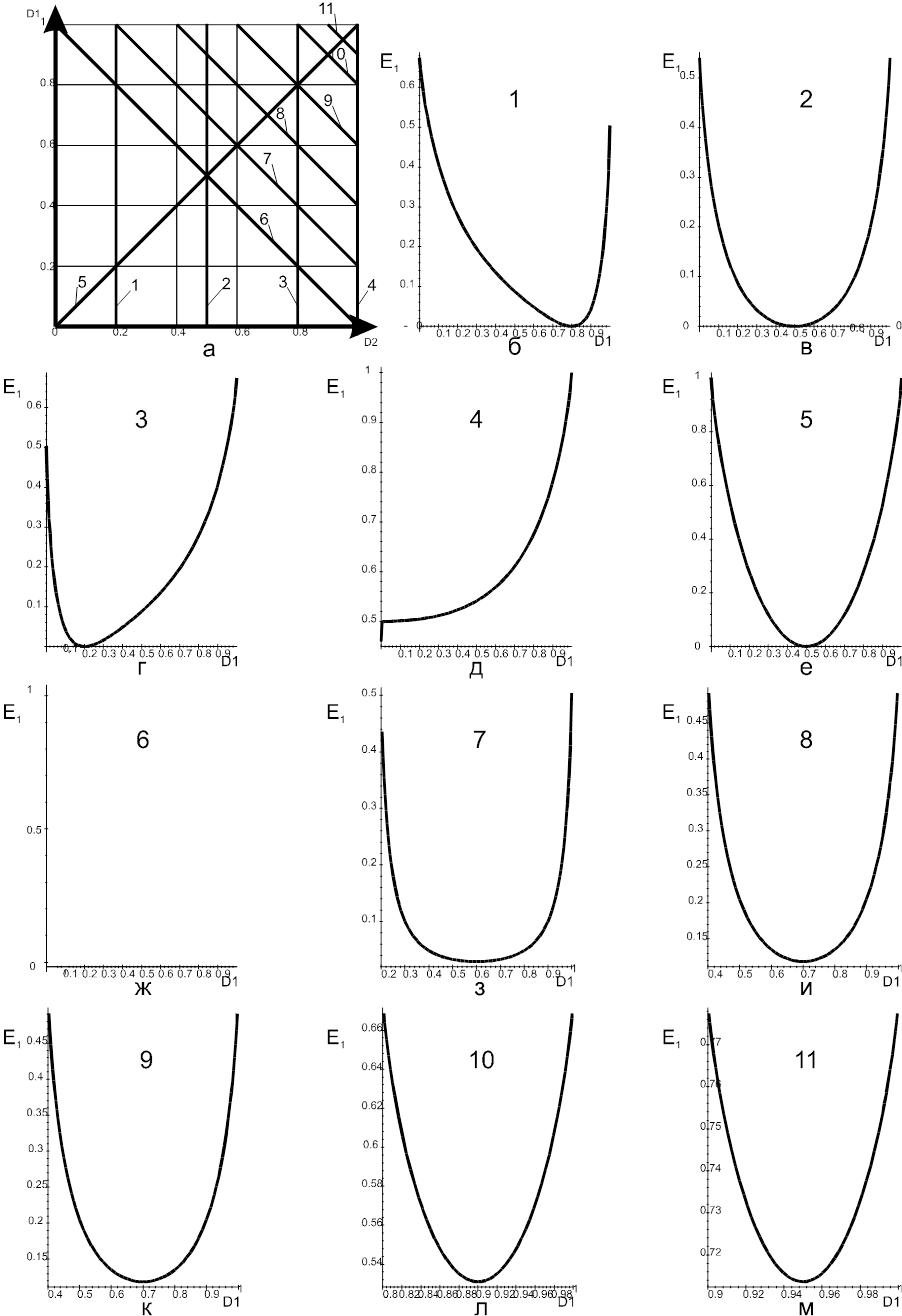
Рис. 3.6. Перерізи поверхні КФЕ: а) місця перерізів; б-м) відповідні перерізи

Аналіз рис 3.6 показує, що для забезпечення практичної цінності  рішень класифікатора, на робочу область визначення функції інформаційного  КФЕ навчання окрім виконання умови реалізації другого принципу адитивності інформації при двохальтернативному рішенні необхідно накладати більш жорсткі обмеження знизу: D₁ ³ 0,5  і  D₂ ³ 0,5, тобто значення  достовірностей у робочій області не можуть бути менше відповідних помилок.

Розглянемо обчислювальний аспект оцінки функціональної  ефективності СК, що навчається, за одержаними в підрозділі 3.4 модифікаціями критерію Кульбака. Після відповідної підстановки (3.5.1) у (3.4.3) отримаємо формулу для обчислення часткової міри Кульбака:

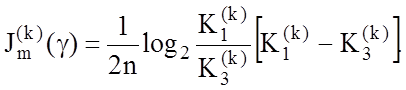                                                          (3.5.3)

Недоліком наведеної формули обчислення критерію оптимізації є можливість появи нескінченних піків, якщо відповідні емпіричні частоти приймають нульові значення. Щоб уникнути необхідність блокувати цього недоліку програмним шляхом при обчисленні такої міри, доцільно використовувати робочу модифікацію формули (3.5.3) у вигляді

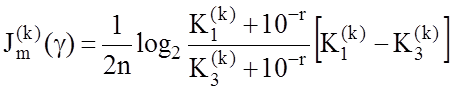                          ,                        (3.5.4)

де       r – число, яке дорівнює двом або кількості цифр у мантисі значення критерію  .

Аналогічно при обчисленні КФЕ за формулою (3.4.4) слід використовувати таку його робочу модифікацію:

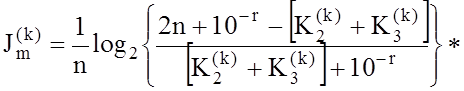
         .         (3.5.5)

Зрозуміло, що залежно від величини числа  rбудуть змінюватися значення критеріїв (3.5.3) або (3.5.5), але це не впливає на положення глобального максимуму в робочій області визначення їх функцій.

3.6 Визначення мінімального обсягу репрезентативної навчальної вибірки

Навчальна вибірка має на практиці скінченний обсяг  n, що обумовлює наявність статистичної похибки  e  між імовірністю  p_i  та емпіричною частотою  k_i n  знаходження значення  i-ї ознаки розпізнавання в своєму контрольному полі допусків  . Верхня оцінка похибки  e = |p_i - |, залежно від кількості випробувань  n, визначається за теоремою Муавра-Лапласа [210]:

        

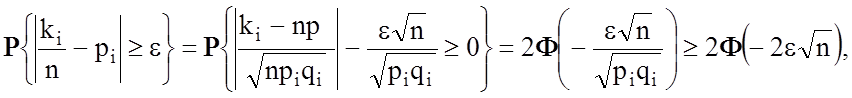
                                                                                                                             (3.6.1)

де       k_i - кількість подій, при яких значення  i-ї ознаки знаходиться в полі            

допусків  ;

           q_i = 1- p_i- імовірність неналежності значення  i-ї ознаки полю допусків  ;

           Ф(...) - функція Лапласа.

Визначення мінімального обсягу  n_min репрезентативної навчальної вибірки здійснимо за умови отримання прийнятних з практичних міркувань статистичної похибки та оперативності алгоритму його обчислення. Ці вимоги є суперечливими, що обумовлює компромісний характер розв’язання задачі. Скористаємося методом динамічного довірчого інтервального оцінювання. Суть методу полягає в побудові після кожного випробування довірчого інтервалу, який оцінює ймовірність  р_і  знаходження  i-ї ознаки в полі контрольних допусків з імовірністю довіри  1 – Q:

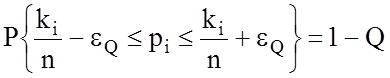                      ,                             (3.6.2)

де      Q -  рівень значущості.

Визначення максимальної (нормальної) похибки   e_Q  при заданому рівні значущості  Q  здійснюється із співвідношення: