Оцінка функціональної ефективності системи керування, що навчається, страница 10

При оцінці ефективності за узагальненим функціонально-статистичним критерієм І.В.Кузьміна (3.1.5) якість функціонування СК , що навчається, визначається її інформаційною спроможністю за умови, що інші складові ефективності враховуються у вигляді зведених витрат. У загальній постановці задача визначення зведених витрат як задача побудови єдиної шкали виміру складових ефективності в даний час ще не знайшла свого розв’язку. Проте, у багатьох практичних випадках достатньо обмежитися оцінкою функціональної ефективності системи при витратах, виражених тільки через її вартісні показники. У першому наближенні ці витрати доцільно виражати через машинний час розв’язання задачі, тому що в НР збір, обробка, передача і збереження інформації здійснюються одним і тим самим методом та на одному і тому самому КТЗ. При цьому природним є введення дискретного часу  n – числа випробувань. Упродовж кожного випробування приймається рішення як про оцінку функціонального стану СК, так і про доцільність подальшого проведення випробувань. Таким чином, число випробувань (машинний час) характеризує економічні  витрати у процесі функціонування СК, що навчається. Мінімальне число випробувань  n_min  визначає деяке граничне значення обсягу навчальної вибірки, яке забезпечує її репрезентативність. Для потенційної системи експлуатаційні витрати на навчання СК залежать пропорційно від мінімального числа випробувань  n_min, яке забезпечує статистичну похибку   < _доп, де   _доп– допустима максимальна похибка при вибраному рівні значущості  Q. Для досягнення такої самої похибки в реальному процесі керування потрібно більше випробувань у порівнянні з потенційною системою. На практиці часто необхідно оцінити на скільки збільшення обсягу навчальної вибірки (при  n > n_min) підвищить достовірність розпізнавання і які витрати необхідні для цього.   

Узагальнений КФЕ навчання СК подамо у вигляді:

                                                         E_I,n = E_I E_n ,                                                  (3.9.1)

де      E_I  - інформаційний критерій, який має нормований вигляд:

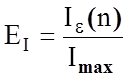                                                         .                                                 (3.9.2)

У виразі (3.9.2)  I_e(n) - умовна інформація (e – інформація), отримана після прийняття рішень з похибкою  e _Q (n) і яка дорівнює різниці:

I_e (n) = H₀ – , (3.9.3)

де     - невизначеність, що залишилася, після прийняття рішень з похибкою  e _Q (n)  (e-ентропія):

                                            = - e_Q (n)log₂  e_Q (n) . (3.9.4)

У виразі (3.9.2)  I_max – максимальне значення інформації, яка знімає  невизначеність, що існувала до прийняття рішення (H_e (n) = 0) , і яка при рівноймовірних гіпотезах (М = 2) дорівнює безумовній ентропії  H₀ = 1.

Критерій економічних витрат  E_n  на навчання розпізнаванню реалізацій одного класу  обчислюється за формулою:

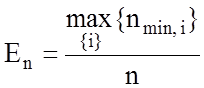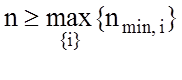                    ,  ;,    (3.9.5)

де 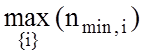    – число випробувань, яке гарантує допустиму статистичну похибку для всіх ознак розпізнавання.

Згідно з виразами (3.9.3) - (3.9.5) і з урахуванням (3.6.5),  критерій (3.9.1) при рівноймовірних гіпотезах і  М = 2 приймає вигляд:

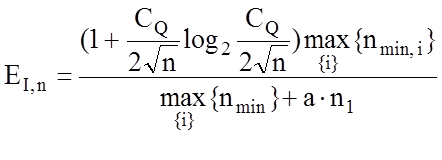                                    ,                          (3.9.6)

де      C_Q - аргумент функції Лапласа при заданому рівні значущості;

          a  – поправочний коефіцієнт, який враховує ціну випробування; 

n₁ = n- 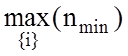 - кількість випробувань після забезпечення репрезентативності навчальної вибірки з гарантованою похибкою  e_Q(n_min ).

Розв’язання задачі вибору достатнього числа випробувань  n*  носить компромісний характер. Приклад вибору числа випробувань  n*  при навчанні розпізнаванню реалізацій одного класу ілюструється рис. 3.11, на якому, як і на рис. 3.7, виділено три області: І - заборонена область, ІІ - компромісна область і ІІІ - область значних економічних витрат.