Оцінка функціональної ефективності системи керування, що навчається, страница 3

Введемо таке позначення величин ознак розпізнавання:  – дійсне значення ознаки знаходиться в полі допусків  d,  – дійсне значення ознаки знаходиться лівіше поля допусків  d та   – дійсне значення ознаки знаходиться правіше поля допусків  d.

Рис. 3.4 ілюструє можливі наслідки контролю  і-ї  ознаки при триальтернативній системі оцінок рішення, яка характеризується такими точнісними характеристиками:

·  помилки першого роду  a₁ = p(g ₂ / m ₁)(рис.3.4а)  і  a₂ = р(g₃ / m₁)  (рис. 3.4б);             

·  помилки другого родуb₁ = р(g₁ / m₂) (рис. 3.4в)  і  b₂=р(g₁ / m₃)    (рис. 3.4г);            

·  помилки третього роду  s₁ = р(g₂ / m₃)  (рис. 2.4д)  і  s₂ = р(g₃ / m₂ )  (рис. 3.4е); 

·  перша достовірність    (рис. 3.4є);

·  друга достовірність    (рис 3.4ж);

·  третя достовірність    (рис 3.4з).

Кількість середньої умовної інформації    про величину  , яка  міститься у векторі  х, за виразом (3.1.4) при  M=3  і рівноймовірних гіпотезах, як відомо,  дорівнює

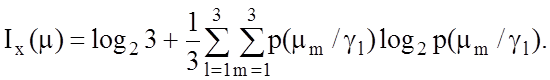                                                (3.3.1)

 

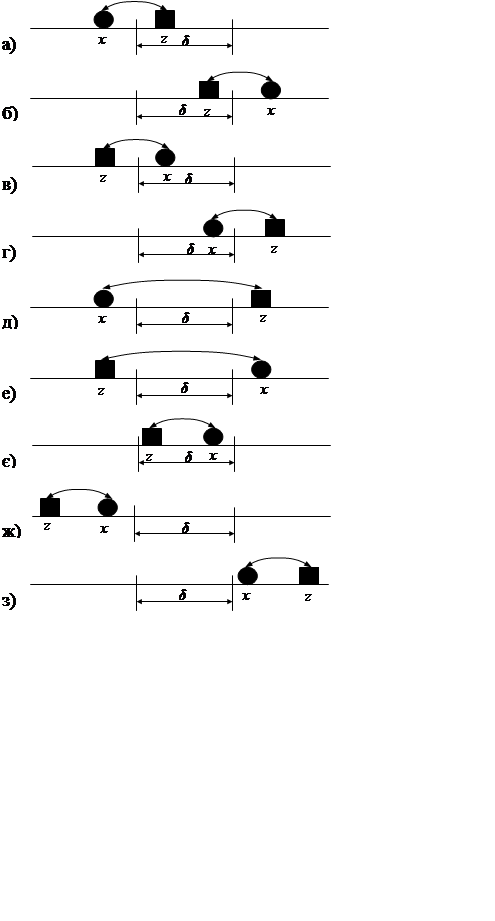Рис. 3.4. Можливі результати оцінки виміру ознаки розпізнавання при 

триальтернативному рішенні

Виразимо ймовірності  p(m_m/g_l) через апріорні за формулою (1.4.1) при   і підставимо їх у формулу (3.3.1), яка після ряду перетворень і підстановки відповідних точнісних характеристик набуває вигляду:

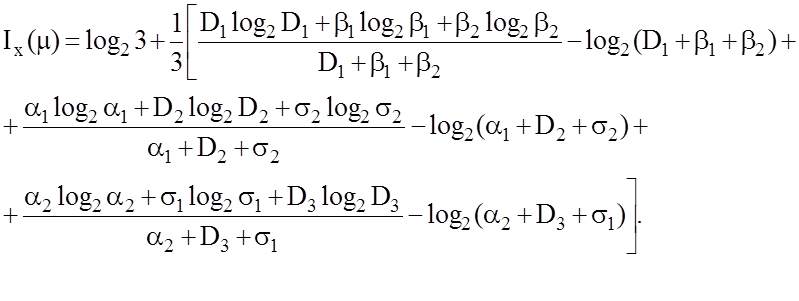            (3.3.2)

Оскільки для точнісних характеристик мають місце такі співвідношення:

D₁ + a₁ + a₂ =1;  D₂ + b₁ + s₁ =1;D₃+ b₂ + s₂ =1, (3.3.3)

то вираз (3.3.2) можна спростити. Для цього припустимо, що при симетричних полях допусків на ознаки розпізнавання помилки одного роду є рівноймовірними, тобто можна покласти  і  Таким чином, замість (3.3.3) маємо

      D₁+2=1; D₂++ =1;  D₃++=1.                        (3.3.4)  

Звідки

                                                D₂ = D₃ = D^¢.                                               (3.3.5)

Тоді, врахувавши (3.3.4) і (3.3.5), вираз (3.3.2) можна спростити:

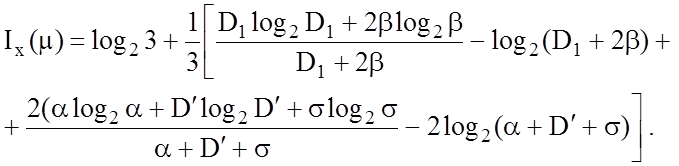                   (3.3.6)

На рис. 3.5 наведено номограму для обчислення кількості умовної інформації при триальтернативній системі оцінок рішеннь.

Рис. 3.5. Номограма обчислення функції    (М=3)

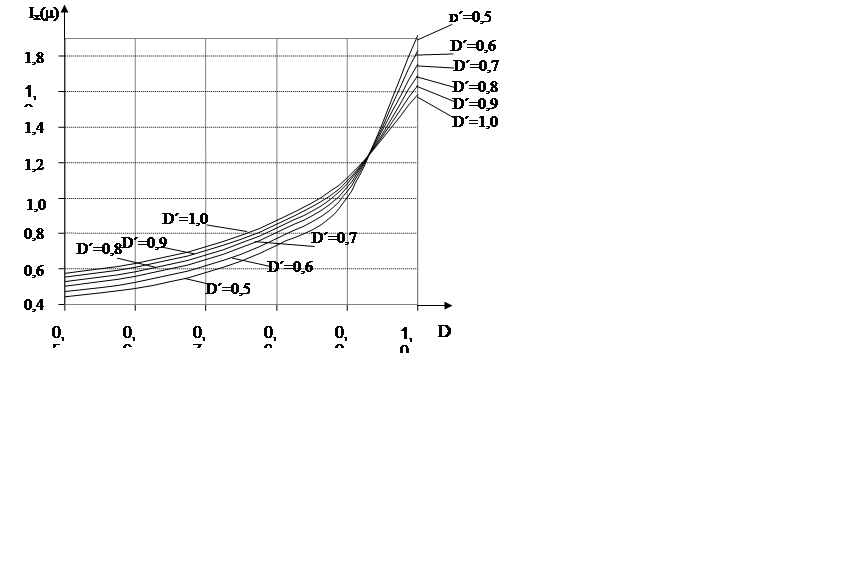Аналіз виразу (3.3.6) підтверджує, що близькі до нуля значення  помилки s  мало впливають на зміну кількості інформації, оскільки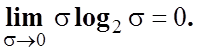   

3.4. Модифікації інформаційної міри Кульбака

Серед логарифмічних статистичних інформаційних мір найбільше розповсюдження знайшла ентропійна міра Шеннона, яка є інтегральною мірою різноманітності. Разом з тим, ще недостатньо уваги приділяється вивченню властивостей міри Кульбака [164], яка дозволяє оцінювати диференційну інформативність ознак розпізнавання. Одержимо робочу формулу для оцінки функціональної ефективності навчання СК розпізнавати реалізації двох образів за Кульбаком та встановимо її зв’язок з точнісними характеристиками процесу навчання в рамках МФСВ.

Нехай  - основна гіпотеза про належність реалізацій  m-го образу  j-му діапазону області класу  , тобто контейнеру 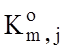 . Тоді  - апостеріорні ймовірності належності контейнеру 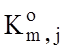 реалізацій відповідно класів   і , де - найближчий сусідній клас до . Відомо, що міра Кульбака розглядається як добуток відношення правдоподібності  L на міру відхилень розподілів імовірностей. У даному випадку, логарифмічне відношення правдоподібності визначимо як

де  k- кількість діапазонів (контейнерів) в яких знаходяться реалізації класів     і  .

За умови побудови контейнерів у радіальному базисі, верхня границя k дорівнює кількості відбудованих на кожному кроці навчання концентрованих контейнерів класу  , центрами яких є вершина еталонного вектора  . Міра Кульбака тоді набуває вигляду:

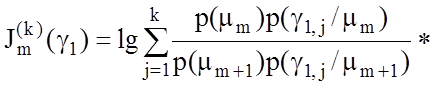
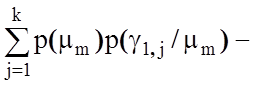
                   * [].               (3.4.1)