Як і в попередніх
випадках, приймемо ![]() , що спростить обчислення і не
вплине на властивості міри (3.4.1). Крім того, за аналогією з мірою Шеннона,
замінемо десятковий логарифм на двійковий. Тоді замість (3.4.1) отримаємо:
, що спростить обчислення і не
вплине на властивості міри (3.4.1). Крім того, за аналогією з мірою Шеннона,
замінемо десятковий логарифм на двійковий. Тоді замість (3.4.1) отримаємо:
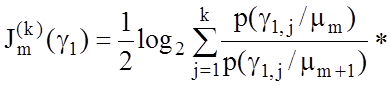
*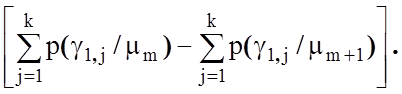 (3.4.2)
(3.4.2)
Оскільки
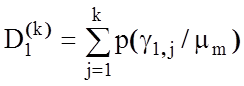 і
і 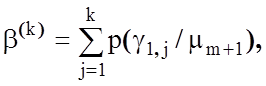
тобто це відповідно перша
достовірність і похибка другого роду при розпізнаванні реалізацій класів ![]() і
і ![]() , які належать побудованому на k-му кроці навчання контейнеру
, які належать побудованому на k-му кроці навчання контейнеру ![]() класу
класу ![]() , то
вираз (3.4.2) подамо у модифікації, яку назвемо частковою мірою Кульбака:
, то
вираз (3.4.2) подамо у модифікації, яку назвемо частковою мірою Кульбака:
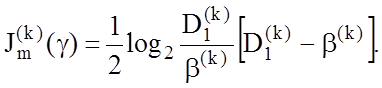 (3.4.3)
(3.4.3)
З метою
узагальнення формули (3.4.3) введемо логарифмічне відношення повної
ймовірності ![]() правильного прийняття рішень про
належність реалізацій класів
правильного прийняття рішень про
належність реалізацій класів ![]() і
і ![]() контейнеру
контейнеру 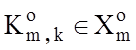 до повної ймовірності помилкового
прийняття рішень
до повної ймовірності помилкового
прийняття рішень ![]() , яке для двохальтернативної
системи оцінок рішеннь має такий вигляд:
, яке для двохальтернативної
системи оцінок рішеннь має такий вигляд:
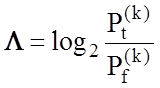
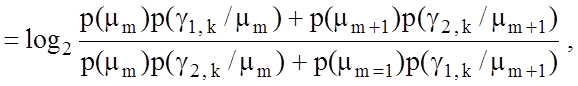
де ![]() – гіпотеза про належність
контейнеру
– гіпотеза про належність
контейнеру 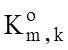 реалізацій класу
реалізацій класу ![]() ;
;
![]() – гіпотеза про належність
контейнеру
– гіпотеза про належність
контейнеру 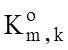 реалізацій класу
реалізацій класу ![]() .
.
При
допущенні, що ![]() , загальна міра Кульбака остаточно набуває
вигляду:
, загальна міра Кульбака остаточно набуває
вигляду:
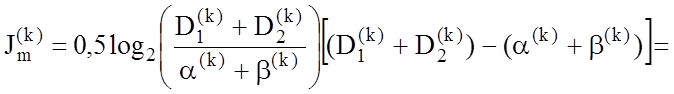
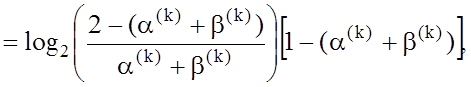 (3.4.4)
(3.4.4)
Модифікації нормованих критеріїв (3.4.3) і (3.4.4) можна подати відповідно у вигляді:
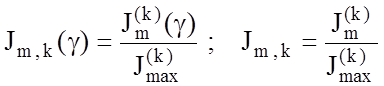 , (3.4.5)
, (3.4.5)
де ![]() – значення критерію при
– значення критерію при ![]() і
і ![]() для формули (3.4.3) і при
для формули (3.4.3) і при ![]() і
і ![]() для формули (3.4.4).
для формули (3.4.4).
У задачах оптимізації параметрів функціонування СК в процесі навчання за МФСВ нормування критеріїв оптимізації не є обов’язковим, оскільки тут розв’язується задача пошуку екстремальних значень параметрів навчання, які відповідають глобальному максимуму КФЕ у робочій області його визначення. Але нормування критеріїв оптимізації є доцільним при порівняльному аналізі результатів досліджень і при оцінці ступеню близькості реальної СК, що навчається, до потенційної.
3.5. Обчислювальний аспект оцінювання функціональної ефективності навчання СК
Обчислювальний аспект оцінювання функціональної ефективності машинного навчання набуває важливого значення в задачах інформаційного синтезу СК і потребує врахування специфіки як їх функціонування, так і їх призначення.
Розглянемо
процедуру обчислення інформаційного КФЕ в рамках алгоритму навчання за МФСВ.
Оскільки інформаційний критерій є мірою різноманітності не менше ніж двох об¢єктів, то для його обчислення
потрібна навчальна матриця, яка складається із векторів-реалізацій двох класів:
![]() і
і ![]()
Нехай клас ![]() є базовим, тобто найбільше
бажаним для ОПР. Тоді належність
вектора-реалізації образу із навчальної матриці класу
є базовим, тобто найбільше
бажаним для ОПР. Тоді належність
вектора-реалізації образу із навчальної матриці класу ![]() приймається за основну гіпотезу g1 , а
неналежність – за альтернативну гіпотезу g2. Алгоритм
оброблення навчальної матриці може бути побудовано за двома способами. За першим способом послідовно
зчитуються реалізації
приймається за основну гіпотезу g1 , а
неналежність – за альтернативну гіпотезу g2. Алгоритм
оброблення навчальної матриці може бути побудовано за двома способами. За першим способом послідовно
зчитуються реалізації ![]() , а потім – реалізації
, а потім – реалізації ![]() . За іншим способом при
кожному випробуванні обробляються
реалізації обох класів.
. За іншим способом при
кожному випробуванні обробляються
реалізації обох класів.
Розглянемо процедуру обчислення модифікації ентропійного інформаційного КФЕ за Шенноном для двохальтернативного рішення при рівноймовірних гіпотезах згідно з формулою (3.2.2). Оскільки інформаційний критерій є функціоналом від точнісних характеристик, то при мінімальному обсязі репрезентативної навчальної вибірки слід користуватися їх оцінками:
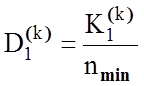 ;
; 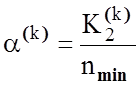
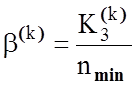 ;
; 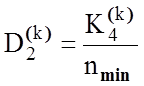 ,
(3.5.1)
,
(3.5.1)
де ![]() - кількість подій, які
означають належність реалізацій образу контейнеру
- кількість подій, які
означають належність реалізацій образу контейнеру 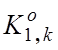 , якщо
дійсно
, якщо
дійсно ![]() ;
;
![]() – кількість подій, які означають
неналежність реалізацій образу контейнеру
– кількість подій, які означають
неналежність реалізацій образу контейнеру 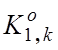 , якщо
дійсно
, якщо
дійсно ![]() ;
;
![]() - кількість подій, які означають належність
реалізацій образу контейнеру
- кількість подій, які означають належність
реалізацій образу контейнеру 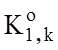 , якщо вони насправді
належать класу
, якщо вони насправді
належать класу ![]() ;
;
![]() - кількість подій, які
означають неналежність реалізацій образу контейнеру
- кількість подій, які
означають неналежність реалізацій образу контейнеру 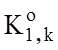 ,
якщо вони насправді належать класу
,
якщо вони насправді належать класу ![]() ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.