Оцінка функціональної ефективності системи керування, що навчається, страница 7

Питання взаємозв'язку оцiнок надiйностi та ефективностi функцiонування складних систем все ще не знайшли належного висвiтлення. Для розв’язання цієї задачі найбiльш придатний функцiональний пiдхiд [191], у рамках якого як комплексний показник надiйностi може бути застосовано коефiцiєнт збереження ефективностi функцiї  К_зе. Цей коефіцієнт, згідно з існуючими стандартами, визначається як вiдношення фактичного значення деякого показника ефективностi цiєї функцiї на заданому перiодi експлуатацiї системи до номiнального значення цього показника, обчисленого за умови, що вiдмови функцiї протягом того самого перiоду не виникали. Стосовно СК, що навчається, як  m-та функцiя розглядається процес навчання розпiзнаванню реалізацій  m-го класу, а як вiдмова  m-ї функцiї - помилкова класифiкацiя реалiзацiї. Таким чином, у рамках функцiонального пiдходу вiдповiдно до iснуючих стандартів розглянемо обчислення коефіцієнта збереження функціональної ефективності    у процесi навчання СК. За МФСВ навчання розпiзнаванню реалізацій  m-го класу закiнчується в момент, коли iнформацiйний КФЕ досягає максимуму    за умови, що  Е_доп £, де  E_доп  і  E_max - допустиме та максимальне значення КФЕ для всiх навчальних функцiй вiдповiдно. Тодi коефіцієнт  К_зе  можна  обчислювати за формулою :

                                                         К_зе ,                                              (3.7.1)

де      - усереднене значення максимумiв КФЕ для  M  навчальних функцiй.    

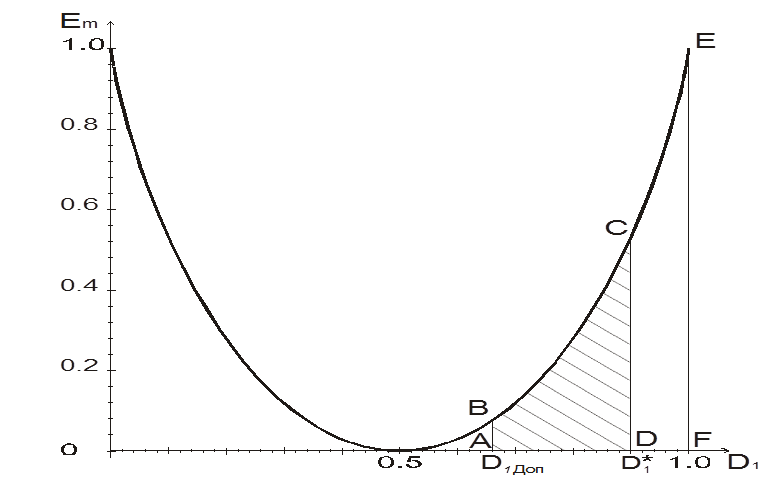
          Обчислення КФЕ для  M=2 i рiвноймовiрних гiпотез здiйснимо за формулою (3.2.2). З урахуванням нелiнiйностi функцiї (3.2.2), наведеної на рис. 3.8,  коефіцієнт  К_зе  визначається як вiдношення усередненої за цикли навчання заштрихованої площi  S_ABCD  до максимальної площi  S_ABEF :

                                               К_зе=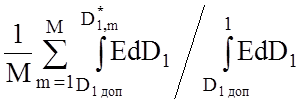                             (3.7.2)

де       - перша достовірність, що визначає значення  критерію  ;

           – перша достовірність, що визначає значення  критерію  .

Рис. 3.8. Область інтегрування КФЕ

Визначення  К_зе  за формулою (3.7.2) потребує обчислення чотирьох iнтегралiв вiд складників, що знаходяться в круглих дужках виразу (3.2.2), якi з урахуванням   = 1 – D₁  i   = 1 – D₂  зводяться до вигляду:

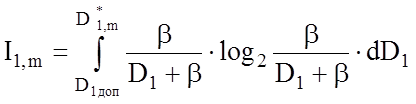                         ,                               (3.7.3)

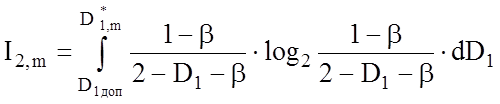                       ,                     (3.7.4)

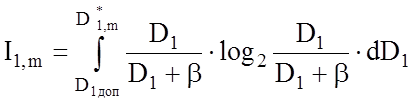                           ,                             (3.7.5)

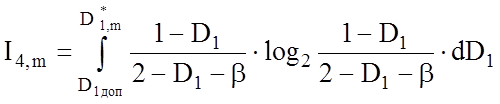                      .                      (3.7.6)

Iнтеграли (3.7.3) i (3.7.4) мають точнi значення:

                            ,

               .

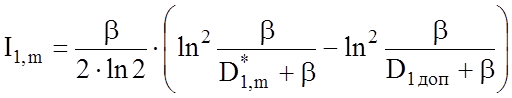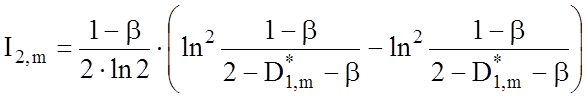Iнтеграли (3.7.5) i (3.7.6) можуть бути обчисленi з деяким наближенням:

    

            

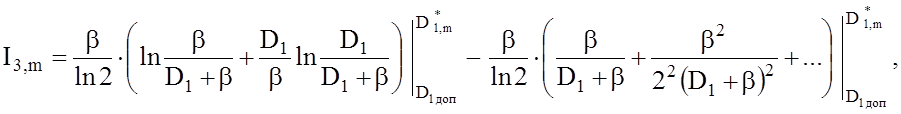
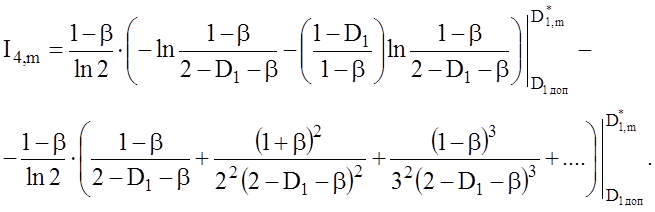
Для оцiнки потрiбної точностi обчислення iнтегралiв  I_3,m,  I_4,m  розглянемо ряд для   | x | < 1:

,

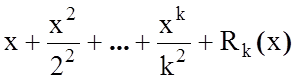де 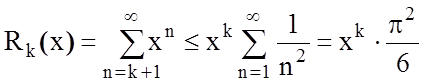 –залишковий член ряду.

Оскільки 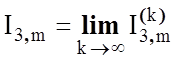, то, зробивши підстановки 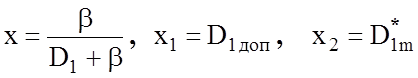,  отримаємо:

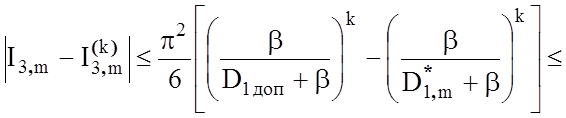
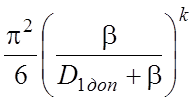        ,         (3.7.7)

де 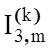      - значення iнтегралу  I_3,m , обчисленi для перших  k  членiв ряду.  

          Якщо задано похибку  e, то  k  вибирається за виразом (3.7.7) за умови:

.

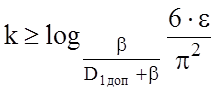Аналогiчно отримаємо:

,

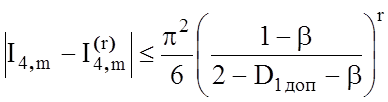де     r - кiлькiсть перших членiв ряду, яка знаходиться для заданої похибки за умови

.

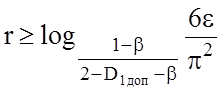Необхідну точнiсть обчислення  К_зе  буде гарантовано при взяттi  s  перших членiв ряду в iнтегралах  I_3,m  і  I_4,m,  де  s=max (k, r). Таким чином, маємо:

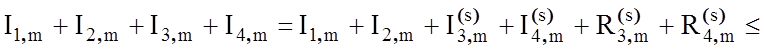
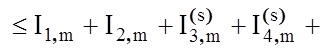
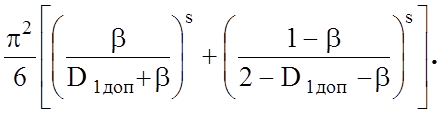
На рис. 3.9 показано залежнiсть коефіцієнта  К_зе  від помилки    для  m=10  i  D_1доп=0.7 за такими даними: =0,94; 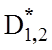=0,88; 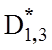=0,91; 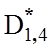=0,86; 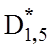=0,90; 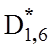=0,92;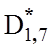=0,88; 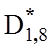=090; 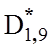=0,90; 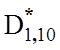=0,92.

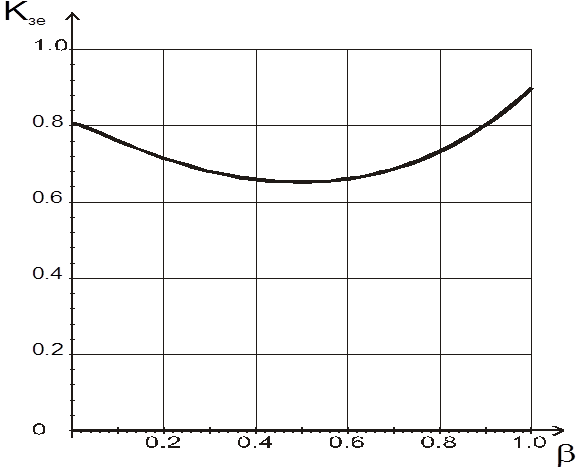
Рис. 3.9.  Залежність  К_зе  від помилки другого роду  b

Аналiз рис. 3.9 показує, що коефiцiєнт  К_зе  в iнтервалi значень    зменшується iз збiльшенням  b, тобто ефективнiсть функцiонування СК знижується. В iнтервалi   збільшення  К_зе  вiдбувається з причини нелiнiйностi та взаємно-неоднозначностi функції  E=f(D₁, D₂), що робить необхiдним виключення цiєї областi значень коефiцiєнта збереження функціональної ефективностi СК, що навчається, із розгляду.