Экономика и менеджмент \ Системы и методы принятия решений

Оцінка функціональної ефективності системи керування, що навчається, страница 6

                                                    .                                            (3.6.3)

З урахуванням властивості функції Лапласа: Ф(х)=1-Ф(-х),   перетворимо (3.6.3) до вигляду:

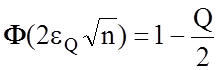                                                    .                                          (3.6.4)

Наприклад, для  Q=0.05за таблицею значень функції Лапласа           [175-178] з урахуванням (3.6.4)  для  Ф(х)= 1- Q / 2 = 0.975, знайдемо значення аргументу функції . Тоді похибка  eQ  змінюється залежно від обсягу навчальної вибірки  n  за гіперболічним законом:

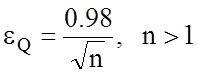                                                       .                                          (3.6.5)

На рис. 3.7 наведено графік функції  eQ = f(n) (крива 1) і умовно виділено три області значень аргументу, які відрізняються крутизною функції. Область  І  є забороненою областю, оскільки похибка перебільшує допустиме значення. Область  ІІІ  характеризується значними економічними втратами при малій швидкості зменшення похибки  eQ. Область  II  є компромісною і охоплює інтервал приблизно від 40 до 100 випробувань. Легко довести, що при різних значеннях рівня значущості  Q  графік функції  eQ = f(n)буде зміщуватися паралельно по вертикалі, не змінюючи свого вигляду.

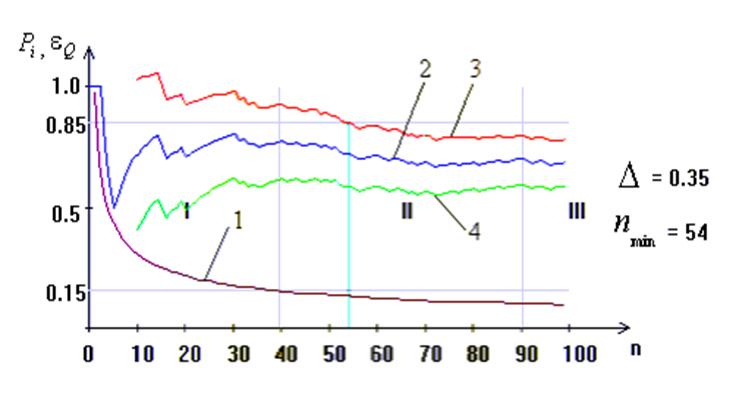
 Рис.3.7. До визначення мінімального обсягу навчальної вибірки:   

                         1 - графік функції  eQ = f(n);

                         2 - графік емпіричної частоти ;

                         3 - верхня межа довірчого інтервалу;

                         4 - нижня межа довірчого інтервалу.

Графічно довірчий інтервал можна побудувати за формулою (3.6.2), обчислюючи для кожного випробування  n  за виразом (3.6.5)  похибку  eQ  i відкладаючи її зверху та знизу від графіка частоти  ki n  (крива 2). При цьому верхня 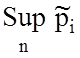  (крива 3) та нижня  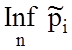 (крива 4) межи довірчого інтервалу при збільшенні числа випробувань, як показано на рис. 3.7, мають тенденцію до зближення з емпіричною частотою.

Для знаходження мінімального числа випробувань  nmin,  яке гарантує прийнятні з практичних міркувань величину похибки і оперативність реалізації алгоритму обчислювання, необхідно задати критерій зупину випробувань. Таким моментом можна вважати випробування, при якому поточний довірчий інтервал накривається заданим інтервалом [0,5±D], де ½D½< 0,5. Останній (правий) перетин заданого інтервалу з однією з меж довірчого інтервалу визначає  випробування   nmin, яке гарантує з імовірністю 1-Q,  що максимальна похибка  eQ   не перебільшує значення функції  =f(n)  при  n=nmin.  Таким чином, за критерієм Парето вибір  nmin  доцільно здійснювати в компромісній області ІІ  (на рис. 3.7  nmin =54) за умови відсутності викидів значень емпіричної частоти до значень, близьких до нуля або одиниці. Для багатьох практичних задач значення  D  визначається з інтервалу  [0,3;0,4] за алгоритмом, наведеним, наприклад, у праці [2].

У загальному випадку, треба будувати довірчі інтервали для всіх  N  ознак і вибирати  nmin  за умови:

  nmin=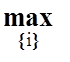(nmin 1, ..., nmin i, ..., nmin N).

При відповідному виборі СКД на незалежні ознаки розпізнавання та забезпеченні умов статистичної сталості та статистичної однорідності функціонально-статистичних випробувань можна вибирати  nmin  за довірчим інтервалом, побудованим для будь-якої однієї ознаки, що значно знижує обчислювальну трудомісткість алгоритму.

3.7. Функціональна ефективність і надійність СК, що навчається

Скачать файл