Оцінка функціональної ефективності системи керування, що навчається, страница 2

Використання узагальненого критерію (3.1.5) є доцільним на етапі апріорного моделювання, коли оцінюється ступінь близькості системи, що проектується, до потенційної, і при структурному синтезі системи. При цьому має місце подвійність розв’язання цієї задачі [59]:

1.  Задана нижня допустима межа ефективності системи. Потрібно синтезувати систему із заданою ефективністю та мінімальною вартістю:

2.  Задана верхня межа вартості системи. Потрібно синтезувати систему із максимальною ефективністю, але не дорожче заданої вартості_.:

Оскільки на етапі апостеріорного моделювання слабо формалізованого процесу класифікаційного керування найбільшої актуальності набуває оцінка саме функціональної ефективності системи, то  вартісну складову критерію ефективності доцільно не розглядати, а нормований інформаційний критерій (3.1.5) тоді набуває вигляду (3.1.1).

3.2. Зв’язок кількості інформації з точнісними характеристиками при двохальтернативних рішеннях

           При двохальтернативних рішеннях (M=2) за основну приймемо статистичну гіпотезу  g₁  про те, що значення ознаки розпізнавання дійсно знаходиться  в полі допусків  d  і як альтернативну їй - гіпотезу  g₂. При цьому мають місце чотири можливих результати оцінки виміру ознаки (рис.3.1), які характеризуються наступними ймовірностями – точнісними характеристиками: помилка першого роду –  (рис. 3.1а); помилка другого роду –  (рис. 3.1б); перша достовірність–   (рис.3.1в) і друга достовірність –     (рис. 3.1г), де  x, z- виміряне та дійсне значення ознаки розпізнавання відповідно.

 

Рис. 3.1 - Можливі результати оцінки виміру ознак

розпізнавання (М = 2) [245]

Розіб’ємо множину значень ознак на області    та  . Область    включає значення, що знаходяться в допуску , а – не в допуску. Тоді можна записати: ,

Виразимо апостеріорні ймовірності   через апріорні за формулою (1.4.1), прийнявши  p(m₁) = p(m₂) = 0,5:

 

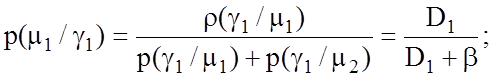
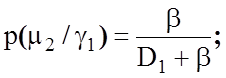
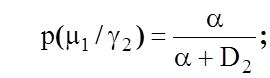
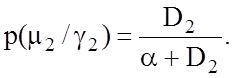                                                      (3.2.1)

Після підстановки (3.2.1) в (3.1.4) отримаємо формулу для обчислення ентропійного КФЕ за Шенноном:

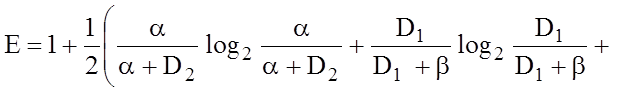
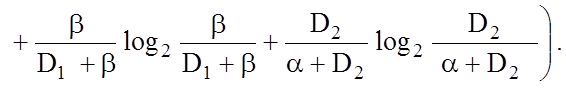                                   (3.2.2)

У загальному випадку побудований за (3.2.2) графік функції    є поверхнею у тривимірному просторі (рис.3.2).

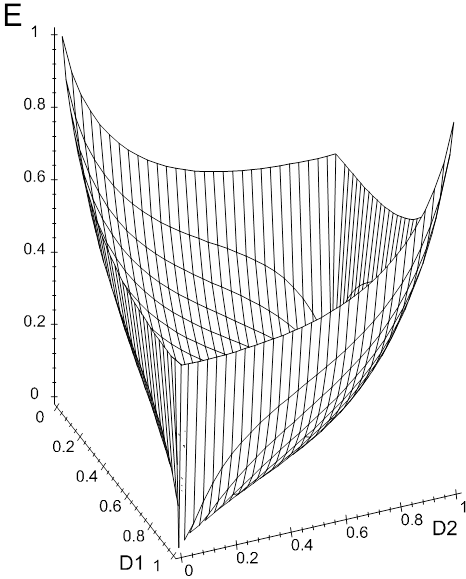
Рис. 3.2. Залежність ентропійного критерію (3.2.2) від точнісних характеристик (М=2)

Як видно з рис. 3.2, функція (3.2.2) є взаємно-неоднозначною. На практиці цей недолік обходять, обмежившись значеннями достовірностей в інтервалі [0,5;1], який характеризує робочу область визначення функції. На рис.3.3 наведено номограму для обчислення критерію (3.2.2)у робочій області визначення його функції.

	Е

 

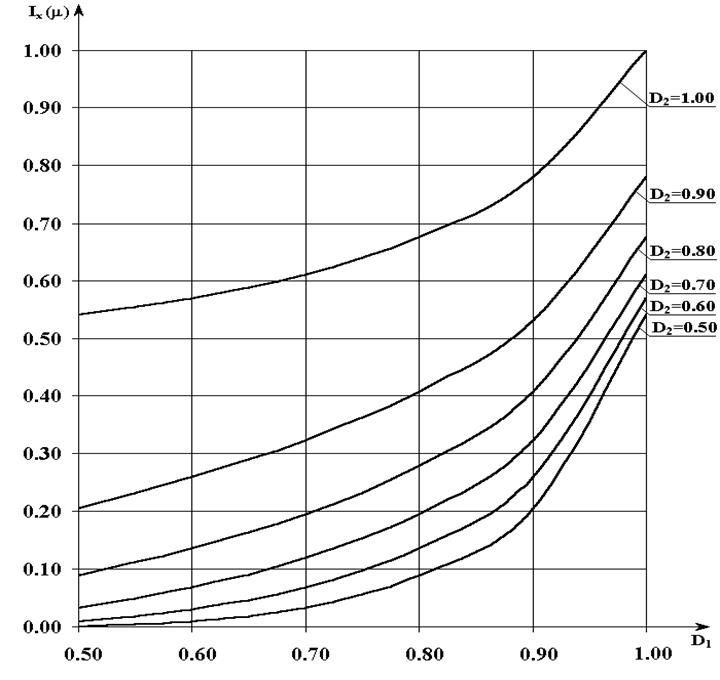
Рис. 3.3. Номограма обчислення ентропійного критерію (3.2.2) у робочій

області його визначення (М=2)

Аналіз номограми (рис.3.3) показує, що при збільшенні як першої, так і другої достовірностей у робочій області визначення функції іформаційного критерію кількість інформації так само збільшується, що знаходиться у відповідності з другим принципом адитивності інформації.

3.3. Зв’язок кількості інформації з точнісними характеристиками при

триальтернативних рішеннях

Практичний інтерес має визначення інформаційної спроможності СК, що навчається, через її точнісні характеристики при триальтернативних рішеннях, де застосовується система оцінок у формі «МЕНШЕ НОРМИ» –«НОРМА» – «БІЛЬШЕ НОРМИ» [245]. Тут, як альтернативні основній гіпотезі  , виступають гіпотеза   про знаходження значення ознаки  лівіше її нижнього допуску «НОРМА» і гіпотеза    про знаходження значення ознаки правіше її верхнього допуску – «НОРМА».