Розділ 10
Неявніметодирозв'язання жорсткихзадач
♦ Жорсткі системи диференціальних рівнянь
♦ Неявні однокрокові та багатокрокові методи
♦ Оцінювання похибок розв'язку
♦ Автоматичний вибір кроку і порядку методу
♦ Об'єднані явно-неявні методи
У цьому розділі розглядаються так звані жорсткі системи диференціальних рівнянь, що описують процеси, які містять швидкі й повільні складові. Функції розв'язку таких систем, як правило, мають дві області: з великими за модулем значеннями похідних та з малими. Це значно ускладнює обчислення розв'язку жорстких систем явними методами, такими як методи Рунге-Кутта чи Адамса, оскільки вони є умовно стійкими, що накладає певні обмеження на вибір кроку інтегрування. Для розв'язання таких систем застосовують неявні методи, у яких для обчислення розв'язку в кожній точці необхідно розв'язувати систему нелінійних рівнянь. Завдяки цьому крок можна вибирати значно більшим, ніж у разі застосування явних методів, розглянутих у розділах 8 і 9.
10.1. Поняттяжорсткостісистеми диференціальнихрівнянь
Для підвищення точності й адекватності математичних моделей складних об'єктів та процесів під час їх побудови потрібно враховувати велику кількість факторів і параметрів. Необхідність врахування в математичній моделі складових із великими і малими значеннями похідних від розв'язку неминуче спричинює так звану жорсткість рівнянь. Добре відомо, що в разі неврахування різного роду «малих величин» у математичних моделях об'єктів і процесів реальна картина явища може бути істотно спотвореною. Тому дослідники змушені включати в моделі велику кількість другорядних, на перший погляд, факторів. У результаті, як правило, підвищується порядок системи рівнянь моделі та її жорсткість. Слід відмітити, що жорсткість є властивістю математичної задачі, а не самого чисельного методу.
Розглянемо спочатку лінійну систему диференціальних рівнянь (10.1) із постійною, тобто не залежною від t, матрицею А:
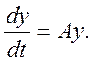 (10.1)
(10.1)
Нехай (![]()
![]() …
…![]() ) — множина
власних чисел матриці А. Система диференціальних рівнянь (10.1) із
постійною матрицею тхт називається жорсткою, якщо система асимптотично стійка
за Ляпуновим, тобто
) — множина
власних чисел матриці А. Система диференціальних рівнянь (10.1) із
постійною матрицею тхт називається жорсткою, якщо система асимптотично стійка
за Ляпуновим, тобто
![]() , k = 1, 2, … m
, k = 1, 2, … m
а відношення найбільшої за модулем дійсної частини власного числа до найменшої за модулем дійсної частини власного числа, тобто:
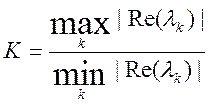 (10.2)
(10.2)
є досить великим.
Для лінійної системи, параметри якої
змінюються в часі, тобто якщо А = A(t), власні
значення ![]() і.
відповідно, число жорсткості К також є функціями t, і визначення
жорсткої системи може бути переформульоване в такий спосіб: система
і.
відповідно, число жорсткості К також є функціями t, і визначення
жорсткої системи може бути переформульоване в такий спосіб: система
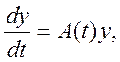 t>0 (10.3)
t>0 (10.3)
називається жорсткою в інтервалі (0,Т), якщо для всіх tє (0,Т), виконується умова
![]() , k = 1, 2, … m
, k = 1, 2, … m
і число
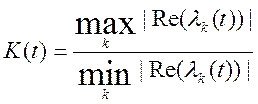
велике.
В основу визначення жорсткості нелінійної системи
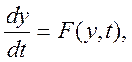 t>0 (10.4)
t>0 (10.4)
покладено попереднє визначення лінійної системи зі змінними коефіцієнтами типу (10.3), де роль матриці A(t) відіграє матриця Якобі J для правої частини системи рівнянь (10.4).
Якщо об'єкт дослідження фізично стійкий, то
![]() , k = 1, 2, … m (10.5)
, k = 1, 2, … m (10.5)
і модулі розв'язку ![]() будуть згасати за умови зростання tіз
швидкістю, пропорційною 1/Re(-λk). Цю величину часто називають локальною сталою
часу системи. Мірою жорсткості задачі Коші є проміжок, в якому лежать її
локальні сталі часу. Число жорсткості, як і число обумовленості матриці А,
характеризується
виразом:
будуть згасати за умови зростання tіз
швидкістю, пропорційною 1/Re(-λk). Цю величину часто називають локальною сталою
часу системи. Мірою жорсткості задачі Коші є проміжок, в якому лежать її
локальні сталі часу. Число жорсткості, як і число обумовленості матриці А,
характеризується
виразом:
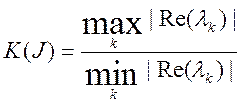 (10.6)
(10.6)
Звичайно кажуть про жорсткість задачі Коші (10.1), якщо ![]() . Однак у
кожному конкретному випадку різні значення K(J) можуть
вважатися великими. Проте максимальний крок обчислень для явних
методів обмежений нерівністю
. Однак у
кожному конкретному випадку різні значення K(J) можуть
вважатися великими. Проте максимальний крок обчислень для явних
методів обмежений нерівністю
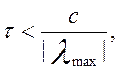 (10.7)
(10.7)
де с - константа, яка залежить від умов задачі, ![]() - максимальне власне число матриці Якобі.
- максимальне власне число матриці Якобі.
Для використання виразів (10.7) і
(10.6) необхідно знати максимальні значення модулів власних чисел ![]() або максимальні та мінімальні значення їх
дійсних частин
або максимальні та мінімальні значення їх
дійсних частин ![]() . Величину
. Величину ![]() можна оцінити зверху за допомогою норми матриці, а їх
дійсну частину — за допомогою сліду матриці Якобі (10.2). Щоб не
обчислювати обернену матрицю
можна оцінити зверху за допомогою норми матриці, а їх
дійсну частину — за допомогою сліду матриці Якобі (10.2). Щоб не
обчислювати обернену матрицю ![]() , малі за
модулем
, малі за
модулем ![]() можна також оцінювати,
виходячи з інтервалу інтегрування Т задачі Коші (10.1), заданого з урахуванням
фізичних властивостей досліджуваного об'єкта чи процесу.
можна також оцінювати,
виходячи з інтервалу інтегрування Т задачі Коші (10.1), заданого з урахуванням
фізичних властивостей досліджуваного об'єкта чи процесу.
Жорсткі системи диференціальних рівнянь є математичними моделями складних об'єктів, великий діапазон зміни часових характеристик яких зумовлений фізичною природою самих об'єктів чи процесів у них. Прикладами моделей таких об'єктів можуть бути моделі, які створюються формальним об'єднанням систем із різними сталими часу (наприклад, моделі інерційного об'єкта і малоінерційного контролера). Однак у загальному випадку жорсткість може проявлятися в результаті об'єднання і взаємодії нежорстких систем. У цьому разі розв'язок об'єднаної системи може істотно відрізнятися від розв'язків окремих систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.