Информатика и выч. техника \ Численные методы в информатике

Неявні методи розв'язання жорстких задач, страница 3

У розбіжності рішення явним методом Ейлера, якщо , можна переконатися, за­програмувавши цей метод у пакеті Mathematical

ln[]:= u[0] = 1;

           t[0] = 0;

           m = 4;

          ;

              Do [{t[n] = t[0] + *n;

                       f[n] = t[n]^2 – 15*u[n]^2; u[n+1] = u[n] + *f[n]} ];

              Do [Print [“n = “, n , “t [“, n, ”] = ”, t[n], “u[“, n, ”] = “, u[n]], {n,0,m} ];

Отримані результати:

n = 0  t[0] = 0    u[0] = 1

n = 1  t[1] = 0.1 u[1] = -0.5

n = 2  t[2] = 0.2 u[2] = -0.874

n = 3  t[3] = 0.3 u[3] = -2.01581

n = 4  t[4] = 0.4 u[4] = -8.10207

Далі скористаємось формулою неявного методу Ейлера (10.8) і запишемо:

а потім послідовно сформуємо і розв'яжемо відповідні нелінійні алгебраїчні рівняння:

    

   

Необхідну послідовність обчислень у пакеті Mathematica можна записати в такий спосіб:

ln[]:= f[t_,r_,u_]:= Block[{x},

              w = FindRoot[r*15*x^2 + x – u – r*t^2 =0, {x,u}];

              y = x/.w[[1]]] ;     

t = 0;   u = 1;

           ;  m = 4;

              Do [Print [“n = “, n , “t  = ”, t, “u = “, u];

                     t = t + ; u1 = u; u = f[t, , u1], {n, 0, m}];

Отримані результати:

n = 0  t = 0    u = 1

n = 1  t = 0.1 u = 0.548962

n = 2  t = 0.2 u = 0.359308

n = 3  t = 0.3 u = 0.263868

n = 4  t = 0.4 u = 0.212276


10.3. Неявнілінійнібагатокроковіметоди

Серед лінійних багатокрокових методів, описаних у розділі 9, можна виділити кілька класів неявних методів, побудованих на сітці з постійним кроком.

10.3.1.НеявнібагатокроковіметодиАдамса-Мултона

Для повноти викладу тут наводяться також методи Адамса-Мултона:

♦  неявний метод першого порядку:

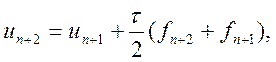
який збігається з неявним методом трапецій (10.9);

♦ неявний метод другого порядку:

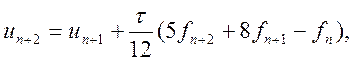                      (10.14)

де ,  і = 0,1,2  — оцінки правої частини розв'язуваного диференціального рівняння в моменти часу , ,;

♦  неявний метод третього порядку:

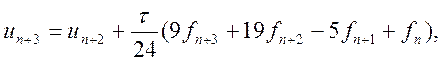           (10.15)

який (за тієї ж точності) значно простіше реалізувати, ніж неявний метод Рун-ге-Кутта четвертого порядку (10.12), оскільки лише один член праворуч від  залежить від шуканого значення

10.3.2.НеявнібагатокроковіметодиРакитського

На відміну від методів Рунге-Кутта методи Ракитського не вимагають багато­разового оцінювання значення похідної:

♦ метод другого порядку:

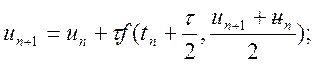                            (10.16)

♦  метод четвертого порядку:

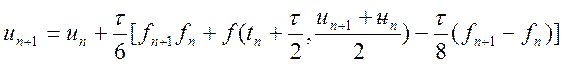    (10.17)


Приклад 10.2

Розв'яжемо неявним методом Ракитського другого порядку (10.16) рівняння:   (див. приклад 10.1). Знайдемо значення  y(0,4) із кроком .

Тоді модифікована програма для пакета Mathematica набуде такого вигляду:

ln[]:= u[0] = 1; t[0] = 0; m = 4; ;

              Do [{t[n] = t[0] + *n; f[n] = t[n+1] +  – 15*((u[n+1]+u[n])/2)^2;

u[n] = u[n+1] - u[n] - *f[n]; 0[n] = u[n] /. U[n + 1  x[n];

              w = NSolve[0[n] = 0, x[n]; u[n+1] = x[n] /. w[[2]];

              Print [“n = “, n , “t [“, n, ”] = ”, t[n], “u[“, n, ”] = “, u[n]], {n,0,m} ];

Отримані результати:

n = 0  t[0] = 0    u[0] = 1

n = 1  t[1] = 0.1 u[1] = 0.334458

n = 2  t[2] = 0.2 u[2] = 0.223827

n = 3  t[3] = 0.3 u[3] = 0.176099

n = 4  t[4] = 0.4 u[4] = 0.155192

10.3.3. НеявнібагатокроковіметодиГіра

На відміну від неявних методів Адамса-Мултона неявні методи Гіра (ди­ференціювання назад) використовують множину попередніх значень функції й лише одну оцінку похідної в поточній точці  базуються вони на застосу­ванні інтерполяційного полінома Лежандра. За постійного кроку обчислень  отримуємо:

♦  метод другого порядку:

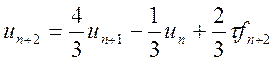                                      (10.18)

♦  метод третього порядку:

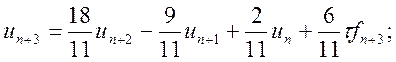                    (10.19)

♦  метод четвертого порядку:

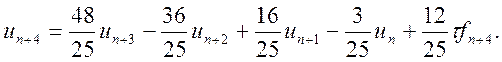      (10.20)          

Однак із практичної точки зору важливими є, насамперед, неявні методи зі змінним кроком обчислень, які дозволяють реалізувати основну перевагу неяв­них методів, що полягає в можливості зміни кроку т в широких межах.

Приклад 10.3

Розв'яжемо неявним методом Гіра другого порядку (10.18) рівняння:  , яке було розв'язане раніше, в прикладі 10.1, неявним методом Ейлера. Неявний метод Гіра називають також методом Шихмана. Потрібно, як і раніше, з кро­ком  знайти значення y(0,4).

Скачать файл