Неявні методи розв'язання жорстких задач, страница 5

m = 0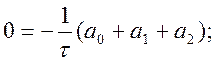          

m = 1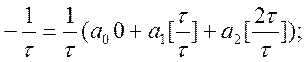     

m = 2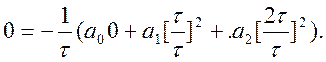        

Вона легко зводиться до такої системи:

    

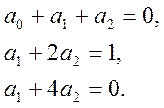
з якої отримуємо , ,       .   Отже, для розглянутого методу за постійного кроку

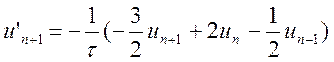 або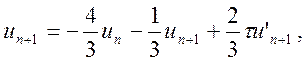        

що збігається з виразом (10.18), відомим як неявний метод Гіра-Шихмана другого порядку. Розглянута методика обчислення  коефіцієнтів формул  наближення є універсальною і дозволяє конструювати неявні методи, які не входять у множину методів Гіра (10.22), що підтверджується наведеним нижче прикладом.

Приклад 10.5

Знайдемо значення коефіцієнтів формули наближення неявного багатокрокового мето­ду, який має вигляд

Порядок формули р дорівнює 2, і шукана система лінійних рівнянь для невідомих кое­фіцієнтів за постійного кроку обчислень набуває вигляду:

m = 0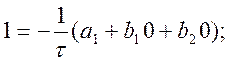          

m = 1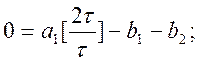     

m = 2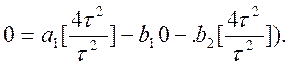        

Із першого рівняння знаходимо коефіцієнт . Друге і третє рівняння перетворяться в систему рівнянь:

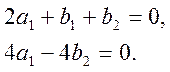
з розв'язку якої знаходимо , тому шукана формула наближення матиме такий вигляд:

10.6. Стійкістьнеявнихметодів

Визначимо умови стійкості неявних методів і порівняємо їх з умовами стійко­сті явних методів, розглянутих у розділах 8 і 9. Почнемо з неявних методів Ей-лера і трапецій, скориставшись методикою аналізу стійкості різницевих рів­нянь, яка базується на визначенні коренів характеристичного рівняння (9.40).

10.6.1.НеявнийметодЕйлера

Скориставшись виразом (10.9) із урахуванням тестового рівняння , формує­мо різницеве рівняння методу  звідки . Від­повідне йому характеристичне рівняння набуває вигляду , корінь якого для  і довільного значення  завжди задовольняє умову стійкості:

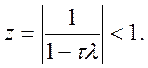                                               (10.37)

10..6.2.       Неявний метод трапецій

На основі виразу (10.10) з урахуванням тестового рівняння  формуємо різницеве рівняння методу:

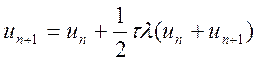  чи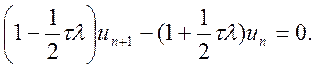 

Відповідне характеристичне рівняння отримуємо у вигляді:

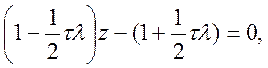
із якого, як і раніше для неявного методу Ейлера, випливає, що для  і довільного значення  умова стійкості завжди задовольняється:

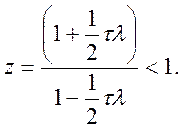                                           (10.38)

10.6.3.НеявнийметодПра-Шихманадругогопорядку

Виходячи з виразу (10.18)

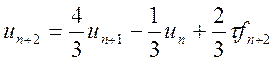
з урахуванням тестового рівнянняформуємо різницеве рівняння методу:

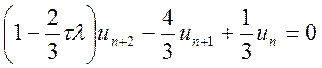
характеристичне рівняння для якого:

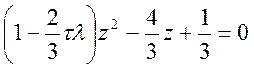
Знайдемо корені цього рівняння:

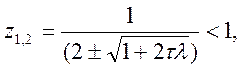                                       (10.39)

тому що, коли , знаменник кореня завжди більше одиниці за значенням (для) або за модулем (для ).

Запропоновано називати А-стійкими розглянуті тут та інші неявні методи, в яких область стійкості у разі розв'язування тестового модельного рівняння містить всю ліву комплексну півплощину , тобто, якщо , роз­в'язок буде асимптотично стійким за будь-якого додатного . Показано також, що ніякий явний лінійний багатокроковий метод не може бути A-стійким і не існує A-стійкого неявного лінійного багатокрокового методу з порядком k > 2.

Дослідження стійкості методу Гіра-Шихмана третього порядку зручніше проводити графічно побудовою годографа стійкості аналогічно визначенню об­ластей стійкості багатокрокових методів (див. рис. 9.2).

Записуючи характеристичне рівняння (10.19) у вигляді , знаходимо з нього  Підста­вивши , отримаємо рівняння межі області стійкості.

Годограф стійкості будується за допомогою пакета Mathematica:

Ln[]:=

Tx4 = Graphics[{ Text [|q|<1, {0.5,0.7}], Text[|q|>1, {3, 0.8}]}];

rg4 = Parametrics Plot [{µx[φ], µy[φ], { φ, 0, 2*Pi},

AxesLabel → {Re τλ, Im τλ }, DisplayFunction → $DisplayFunction];

Л  -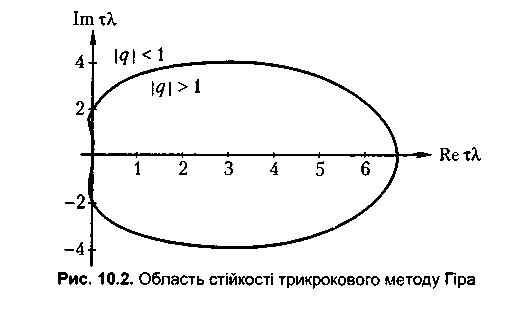

На відміну від попереднього прикладу, існують точки межі області стійкості, розташовані в лівій півплощині. Тому метод третього порядку не є A-стійким.

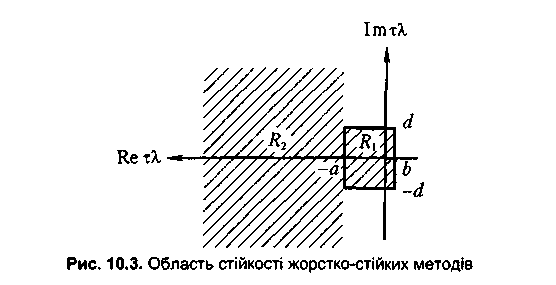
Для неявних методів з порядком k> 2 вимоги A-стійкості послаблюються. Вводиться поняття жорстко-стійких методів (рис. 10.3), для яких їх область стій­кості у разі розв'язання тестового рівняння містить не всю ліву півплощину , а тільки області R₁і R₂, де R₁визначається умовою

                                                         (10.40)

a R₂,— умовою

  a.>0, d>0,                                    (10.41)