Неявні методи розв'язання жорстких задач, страница 2

Уперше поняття жорсткості системи диференціальних рівнянь було введено у зв'язку з труднощами, що виникали під час чисельного інтегрування цих рів­нянь явними методами. Розв'язування системи з малим кроком, зумовленим співвідношенням (10.7), приводить до того, що після згасання перехідних проце­сів, обумовлених «швидкими» складовими розв'язку, будь-яка спроба збільшення кроку інтегрування зумовлює експоненціальне зростання похибки розв'язку че­рез втрату його стійкості. Тому були розроблені спеціальні неявні методи чи-

сельного розв'язання жорстких рівнянь; інтерес до них і область їх застосування беззупинно зростають. Основна мета використання таких методів — забезпечити можливість зміни кроку обчислень у широких межах і забезпечити незалеж­ність результатів від вихідних даних на різних відрізках розв'язку.

Жорстку задачу іноді називають задачею з дуже рознесеними сталими часу чи задачею з великою константою Ліпшиця, під якою розуміють норму матриці Якобі для правої частини диференціального рівняння (10.1). Систему можна вважати жорсткою, якщо коефіцієнт жорсткості (10.6) задовольняє нерівність . Однак у практичних задачах, наприклад під час моделювання проце­сів керування, електричних і електронних ланцюгів, процесів хімічної кінетики та ін., коефіцієнт жорсткості часто досягає значень 10⁶ -10⁸.

10.2. НеявніметодиЕйлераіРунге-Кутта

Поняття неявних методів було введене під час розгляду методів розв'язання дифе­ренціальних рівнянь (див. підрозділ 8.2). Це методи, формули яких містять шука­ні значення наближення у лівій і правій частинах.

Наприклад, для неявного методу Ейлера справедлива формула

                                                    (10.8)

де  —значення правої частини розв'язуваного диференціального рів­няння (10.1) у момент часу  для якого власне і шукається наближення . Формула (10.8) має наочну графічну інтерпретацію (рис. 10.1), аналогічну до тієї, яка була наведена для явного методу.

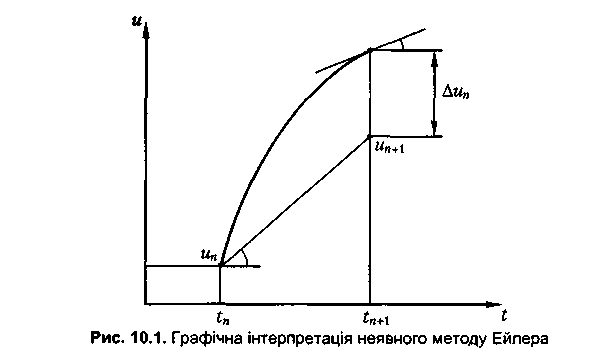
На рис. 10.1 показано процес знаходження чергового наближення. Для цьо­го з початкової точки з координатами проводиться дотична до функції точного розв'язку в точці , у результаті чого отримують наступну точку наближення . Слід відмітити, що для опуклої функції точного

розв'язку значення наближення неявним методом Ейлера будуть менше від точних значень, а значення наближення явним методом перевищуватимуть точ­ні значення. Тому природним є бажання усереднити наближення, щоб отри­мати більш точний результат:

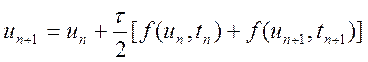                                     (10.9)

Формула (10.9) відома як формула неявного методу трапецій, і вона деякою мірою відповідає формулі (8.35) явного методу Хейна, в якому точне значення похідної в кінці інтервалу обчислень замінено на наближене значення .

З скороченого ряду Тейлора для  отримаємо неявні методи Рунге-Кутта:

♦  другого порядку:

                                                 (10.10)

де

      

♦  третього порядку:

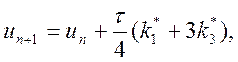                                      (10.11)

де

    

♦  четвертого порядку:

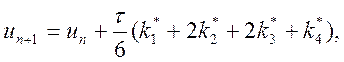                      (10.12)

де

   

Порівнюючи вирази для неявних методів (10.10) - (10.12) із формулами явних методів (8.24) - (8.30), неважко побачити їх подібність, за винятком того, що точки початку і кінця інтервалу помінялися місцями і відлік незалежного пара­метра tведеться у зворотному напрямку (назад). Користуючись принципом ду­альності, за аналогією з формулами (8.23) - (8.30) можна записати формули не­явних вбудованих методів. Як і раніше, глобальна похибка неявного методу k-го порядку оцінюється величиною , а локальна —величиною .

Застосування неявних методів Ейлера та Рунге-Кутта перетворює задачу інтегрування жорстких диференціальних рівнянь у задачу розв'язання неліній­них алгебраїчних рівнянь (10.8), (10.10) - (10.12) відносно . У цьому разі складність нелінійного алгебраїчного рівняння зростає з ростом кількості оці­нок параметрів k, що використовується у різних формулах.

к

Приклад 10.1

Розв'яжемо явним і неявним методами Ейлера рівняння  з початковими умовами із кроком . Знайдемо значення  y(0,4) і порівня­ємо отримані результати.

Вибране значення кроку  перевищує в 1,5 разу допустимий крок обчислень явним методом Ейлера, який згідно з (10.7) дорівнює τ = 0,066(6), тому що  і с = 2.