Крім того, для ![]() ,, забезпечується
задана точність. Суть вимоги
,, забезпечується
задана точність. Суть вимоги ![]() полягає
в тому, що за великих
полягає
в тому, що за великих ![]() забезпечується згасання «швидких» складових розв'язку, а за малих
забезпечується згасання «швидких» складових розв'язку, а за малих ![]() , якщо
, якщо ![]() , зберігається
необхідна точність
«повільних» складових розв'язку.
, зберігається
необхідна точність
«повільних» складових розв'язку.
До жорстко-стійких методів належать методи Гіра і Брайтона, неявні методи Ракитського і неявні методи Рунге-Кутта, коли k> 2.
Наведемо умови стійкості неявних методів Рунге-Кутта:
♦ другого порядку:
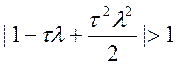 (10.42)
(10.42)
♦ третього порядку:
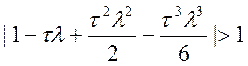 (10.43)
(10.43)
♦ четвертого порядку:
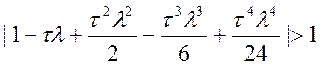 (10.44)
(10.44)
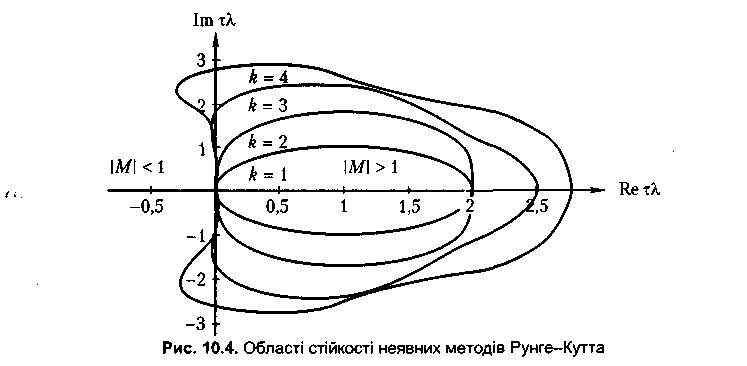
Порівнюючи
умови (10.42) - (10.44) з умовами стійкості явних методів тих же порядків
(8.59), можна зробити висновок, що області стійкості неявних методів
Рунге-Кутта можуть бути побудовані з областей стійкості явних методів (рис.
8.7) заміною ![]() на
на ![]() і зміною знака нерівності. Однак при цьому змінюється
і правило оцінки стійкості розв'язків: тепер точки всередині годографа
характеризують нестійкі розв'язки, а поза годографом — стійкі. Області стійкості
багатокрокових неявних методів змінного порядку Гіра, отримані на підставі
виразу (10.21), наведені на рис. 10.5.
і зміною знака нерівності. Однак при цьому змінюється
і правило оцінки стійкості розв'язків: тепер точки всередині годографа
характеризують нестійкі розв'язки, а поза годографом — стійкі. Області стійкості
багатокрокових неявних методів змінного порядку Гіра, отримані на підставі
виразу (10.21), наведені на рис. 10.5.
Тут, як
і на рис. 10.4, точки всередині годографа характеризують нестійкі розв'язки, а
поза годографом — стійкі. На рисунку видно, що методи першого і другого
порядків (k<
2) є A-стійкими, тобто області їх абсолютної стійкості включають
всю ліву півплощину ![]() , де
, де ![]() — власні
значення матриці Якобі для правої частини розв'язуваного рівняння. Для k= 3,..., 6
вони з одного боку
— власні
значення матриці Якобі для правої частини розв'язуваного рівняння. Для k= 3,..., 6
вони з одного боку ![]() -стійкі, тому що області їх абсолютної
стійкості включають необмежений клин
-стійкі, тому що області їх абсолютної
стійкості включають необмежений клин ![]() , а з
іншого — жорстко стійкі, оскільки області їх стійкості обмежені частиною лівої півплощини,
при цьому в околі початку координат забезпечується не лише стійкість, але й
точність.
, а з
іншого — жорстко стійкі, оскільки області їх стійкості обмежені частиною лівої півплощини,
при цьому в околі початку координат забезпечується не лише стійкість, але й
точність.
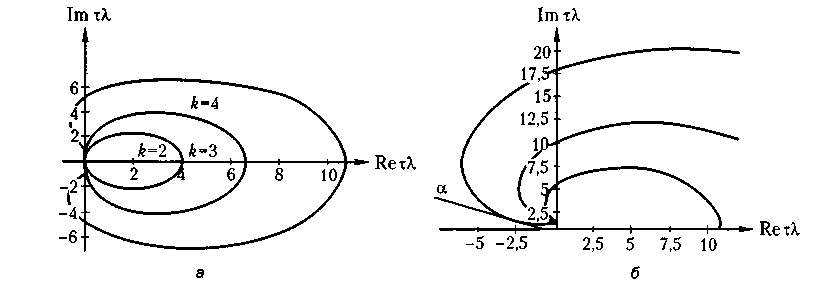
Рис. 10.5. Області стійкості k-крокових методів Гіра:
а — годографи методів першого — четвертого порядків; б — годографи методів четвертого — шостого порядків
Жорстка
стійкість характеризується максимальним кутом дотичної ![]() до
кривої годографа в лівій півплощині (для
до
кривої годографа в лівій півплощині (для ![]() ). У табл.
10.1 наведені значення кута для формул Гіра різних порядків
). У табл.
10.1 наведені значення кута для формул Гіра різних порядків ![]() за відносної зміни кроку обчислень
за відносної зміни кроку обчислень ![]() .
.
Таблиця 10.1. Значення кута нахилу дотичної а для годографів методів Гіра різних порядків
|
Зміна кроку q |
Порядок методу k |
|
1 2 3 4 5 6 7 |
|
|
1 1.01 1.02 1.05 1.1 1.2 1.5 2.0 |
90o 90o 86o 74o 52o 18o 0o 90o 90o 85o 72o 48o 10o 0o 90o 90o 85o 71o 45o 1o 0o 90o 90o 83o 65o 32o 0o 0o 90o 89o 81o 55o 1o 0o 0o 90o 87o 70o 25o 0o 0o 0o 90o 75o 25o 0o 0o 0o 0o 90o 50o 0o 0o 0o 0o 0o |
Виходячи
з даних табл. 10.1, можна зробити висновок, що в процесі обчислень часовий
крок потрібно змінювати поступово (а не збільшувати або зменшувати
вдвічі, як це прийнято), якщо необхідно використовувати неявні методи високих
порядків. Підвищити порядок ![]() -стійких методів можна,
якщо у формулу наближення ввести другу похідну, як це зроблено в методах
Енрайта:
-стійких методів можна,
якщо у формулу наближення ввести другу похідну, як це зроблено в методах
Енрайта:
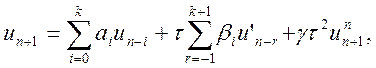 (10.45)
(10.45)
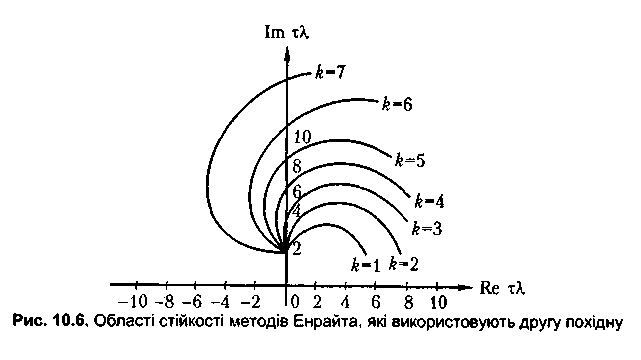
при цьому жорстка стійкість зберігається аж до методу з порядком k = 12 (рис. 10.6). Друга похідна функції у формулі (10.45) обчислюється за допомогою матриці Якобі для правої частини рівняння так:
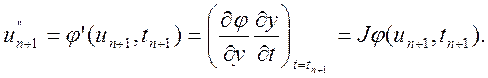
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.