Оскільки у
формулі (10.18) застосовуються значення розв'язку, отримані вдвох попередніх точках, скористаємося
результатами прикладу 10.1 — значеннями ![]() та
та ![]() . Це не
дуже точне значення впливає на точність усіх наступних обчислень. Тоді модифікована програма
для пакета Mathematica набуде такого вигляду:
. Це не
дуже точне значення впливає на точність усіх наступних обчислень. Тоді модифікована програма
для пакета Mathematica набуде такого вигляду:
ln[]:= u[0] = 1;
t[0] = 0; u[1] = 0.548962; m = 4; ![]() ;
;
Do
[{t[n] = t[0] + ![]() *n; f[n] = t[n+1]^2 –
15(u[n+1]^2;
*n; f[n] = t[n+1]^2 –
15(u[n+1]^2;
u[n] = u[n+1] – 4*u(n)/3 + u[n-1]/3 - ![]() *2*f[n]/3;
*2*f[n]/3;
0[n] = u[n] /. U[n + 1] ![]() x[n]; w = NSolve[0[n] =
0, x[n]];
x[n]; w = NSolve[0[n] =
0, x[n]];
u[n+1] = x[n] /. w[[2]];
Print [“n = “, n , “t [“, n, ”] = ”, t[n], “u[“, n, ”] = “, u[n]], {n,1,m} ];
Отримані результати:
n = 1 t[1] = 0.1 u[1] = 0.548962
n = 2 t[2] = 0.2 u[2] = 0.307021
n = 3 t[3] = 0.3 u[3] = 0.194531
n = 4 t[4] = 0.4 u[4] = 0.146298
10.4. Багатокроковінеявніметодизмінногопорядку ізмінногокроку
Узагальнюючи формули (10.18)—(10.20), можна записати такий вираз для неявного методу «диференціювання назад», відомого як формула Гіра зі змінним кроком t та змінним порядком k:
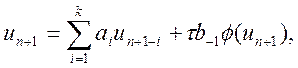 k ≤ 6, (10.21)
k ≤ 6, (10.21)
звідки легко знаходиться уточнена формула апроксимації похідної:
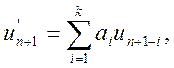 k ≤ 6,
(10.22)
k ≤ 6,
(10.22)
Коефіцієнти
![]() у
формулах (10.21) і (10.22), як буде показано нижче, обчислюють з урахуванням
зміни кроку в процесі обчислень:
у
формулах (10.21) і (10.22), як буде показано нижче, обчислюють з урахуванням
зміни кроку в процесі обчислень:
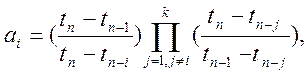 j =
1,2,…, k (10.23)
j =
1,2,…, k (10.23)
Оскільки вираз (10.21) відповідає нелінійному алгебраїчному рівнянню (невідома величина м„+і присутня в його лівій і правій частинах одночасно), то для покращення збіжності методу Ньютона-Рафсона знаходять початкове наближення у вигляді прогнозованого значення:
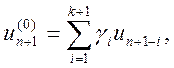 (10.24)
(10.24)
де коефіцієнти
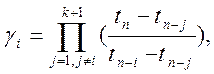 i = 1,…, k+1.(10.25)
i = 1,…, k+1.(10.25)
Відома формула диференціювання назад Брайтона (BDF) відрізняється від формули Гіра (10.21) тим, що в ній замість значень функції використовують лише їх скінченні різниці:
![]() i = 1,2,…, k(10.26)
i = 1,2,…, k(10.26)
Тоді замість виразів (10.22) і (10.24) отримуємо еквівалентні співвідношення:
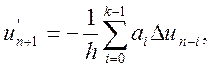
(10.27)
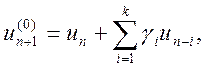
в яких коефіцієнти взаємозалежні:
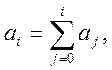
(10.28)
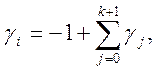
Якщо від перших скінченних різниць функції перейти до різниць вищих порядків, то отримаємо співвідношення:
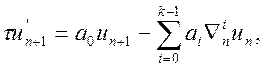 (10.29)
(10.29)
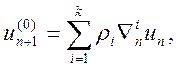 (10.30)
(10.30)
в яких коефіцієнти й скінченні різниці високих порядків обчислюються за такими рекурентними формулами:
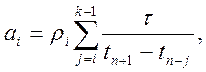
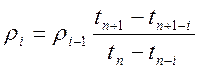 ,
, ![]() ,
(10.31)
,
(10.31)
![]()
10.5. Обчисленнякоефіцієнтівнеявних формулнаближення
Для ілюстрації методики обчислення значень коефіцієнтів використаємо формулу (10.22):
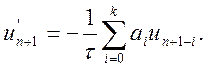
На її основі
побудуємо систему лінійних рівнянь для обчислення значень ![]() , по черзі застосовуючи цю формулу до послідовності
поліномів:
, по черзі застосовуючи цю формулу до послідовності
поліномів:
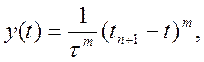 m
= 0,1,2,…,k
m
= 0,1,2,…,k
Формула (10.22) дозволяє знайти точні значення похідних від цих поліномів
![]()
поки їх порядок не перевищує порядок самої формули k. Для поліномів зростаючого порядку послідовно обчислюємо значення функції та її похідної:
m = 0 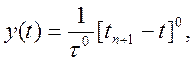
![]()
m = 1 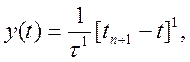
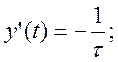
m = 2 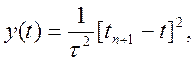
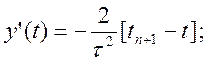 (10.32)
(10.32)
… … … … … … …
m = k 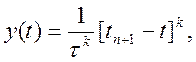
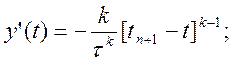
Підставляючи знайдені значення (10.32) в розгорнуту формулу (10.22)
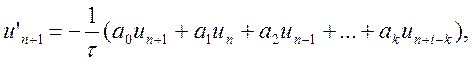
будуємо шукану систему лінійних рівнянь відносно невідомих коефіцієнтів:
m = 0 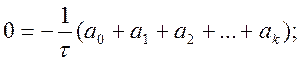
m = 1 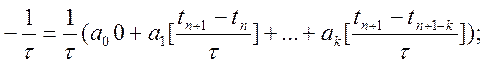
… … … …
m = 0 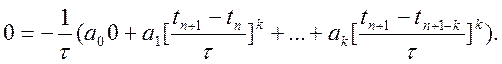
Застосовуючи матричну форму запису з визначником Ван-дер-Монда, остаточно отримуємо:
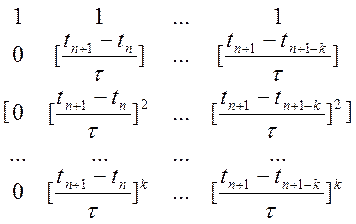
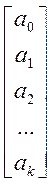 =
= ![]() (10.33)
(10.33)
звідки
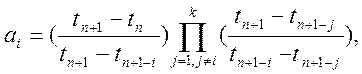 i =
1,2,…, k (10.34)
i =
1,2,…, k (10.34)
Аналогічно для обчислення коефіцієнтів формули прогнозу побудуємо систему лінійних рівнянь (10.24):
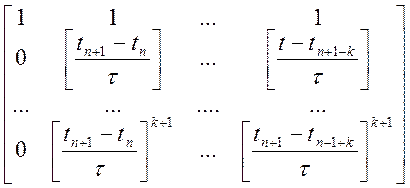
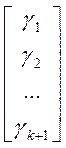 =
= 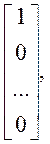 (10.35)
(10.35)
з якої отримаємо значення
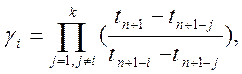 (10.36)
(10.36)
що збігаються з (10.25).
Приклад 10.4
Знайдемо коефіцієнти формули неявного багатокрокового методу Гіра, яка відповідно до виразу (10.22) має вигляд:
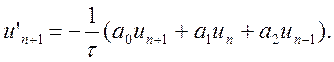
Оскільки порядок формули дорівнює 2, то шукана система лінійних рівнянь відносно невідомих коефіцієнтів за постійного кроку формується у вигляді:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.