Оцінкалокальноїпохибки іорганізаціяобчислень
Як було відмічено в розділі 9,
головний член локальної похибки наближення багатокрокового лінійного методу ![]() -го порядку визначається першим
неврахованим членом відповідного еквівалентного ряду Тейлора:
-го порядку визначається першим
неврахованим членом відповідного еквівалентного ряду Тейлора:
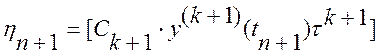
Цей вираз, що містить похідні високих порядків від розв'язку, можна безпосередньо використовувати у випадках, коли застосовуються формули методів Гіра змінного порядку і змінного кроку, (10.29) і (10.30), виражені через скінченні різниці високих порядків, при цьому:
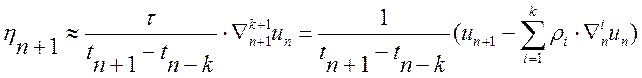 (10.46)
(10.46)
У таких випадках принципово можливе одночасне паралельне оцінювання похибки обчислень для кожного із стійких методів із порядками k= 1, 2,..., 6, що полегшує вибір найбільш ефективного з них на кожному кроці обчислень.
Якщо ж застосовуються формули методів Гіра (10.22) або (10.27), в яких використовуються значення функції або її перші скінченні різниці, то доречніше оцінювати похибку вбудованими методами (див. підрозділ 8.4). При цьому більш зручним, з одного боку, є використання формул прогнозу (10.24), (10.27) і (10.30), а з іншого, — формул наближень (10.22), (10.27) і (10.30). У результаті похибка виражається через різницю прогнозованого і обчисленого значень:
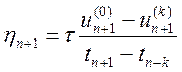 (10.47)
(10.47)
Оцінка похибки з використанням розв'язків із різними кроками, яка описана в розділі 8, для методу змінного кроку принципово неможлива.
Нагадаємо, що прогнозоване
значення ![]() використовується також у разі застосування
методу Ньютона для обчислення наближення
використовується також у разі застосування
методу Ньютона для обчислення наближення ![]() під час
розв'язання нелінійних алгебраїчних рівнянь (10.22), (10.27) і (10.30). З метою
економії часу часто застосовують модифіковану процедуру Ньютона, для якої
обчислення матриці Якобі та розв'язання отриманої лінійної системи методом LU- розкладання виконується лише один раз на
кожному кроці. Це, звичайно, призводить до збільшення значення локальної
похибки і, як наслідок, до зростання кількості виконуваних кроків на заданому
інтервалі, однак загальний час розрахунку може виявитися меншим, тому що
істотно зменшуються витрати на кожен із таких кроків.
під час
розв'язання нелінійних алгебраїчних рівнянь (10.22), (10.27) і (10.30). З метою
економії часу часто застосовують модифіковану процедуру Ньютона, для якої
обчислення матриці Якобі та розв'язання отриманої лінійної системи методом LU- розкладання виконується лише один раз на
кожному кроці. Це, звичайно, призводить до збільшення значення локальної
похибки і, як наслідок, до зростання кількості виконуваних кроків на заданому
інтервалі, однак загальний час розрахунку може виявитися меншим, тому що
істотно зменшуються витрати на кожен із таких кроків.
Звичайно, така організація обчислень можлива за умов, які практично збігаються з загальними умовами розв'язання диференціального рівняння (див. підрозділ 8.1) і полягають в тому, що права частина диференціального рівняння повинна бути принаймні двічі диференційована і мати обмежені значення. До того ж для всіх tфункція
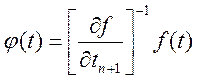 (10.48)
(10.48)
повинна бути монотонною.
У комерційних програмах, які реалізують неявні методи змінного порядку і кроку Гіра, звичайно передбачаються засоби для розв'язування конкретної задачі з заданою точністю шляхом вибору деяких констант (опцій), які визначають кількість допустимих ітерацій Ньютона (чи оцінок матриці Якобі) на кожному кроці (від однієї до десятків) і кількості кроків, на яких матриця Якобі не змінюється (від одного до кількох).
10.8. Автоматичнийвибіркроку іпорядкуметоду
Суть методу змінного порядку і змінного кроку полягає в тому, що ці величини, залежно від виду функції розв'язку, погоджено вибираються автоматично на кожному кроці з метою мінімізації загальних витрат комп'ютерних ресурсів на розв'язання задачі з заданою користувачем точністю.
Оскільки порядок методу безпосередньо залежить від кількості визначених і збережених величин, то змінювати його не складно, прогнозуючи локальні похибки для методів різних порядків і вибираючи той, для якого оцінка похибки мінімальна. Потім для обраного порядку методу можна оцінити максимальний крок, виходячи з умов забезпечення заданої точності розв'язку і дотримання умов його стійкості. Є принаймні дві можливі реалізації описаного вище підходу.
10.8.1. Алгоритм із довільним вибором порядку методу
Застосовується у випадках, коли використовуються формули методів Гіра змінного порядку і змінного кроку (10.29) і (10.30), виражені через скінченні різниці високих порядків. Цей алгоритм передбачає виконання таких кроків.
1.На кожному кроці за формулами
(10.46) прогнозується похибка розв'язку
для методів 1, 2, k+
1 порядків:
![]() (10.49)
(10.49)
2. Вибирається найменша з можливих похибок:
![]() (10.50)
(10.50)
яка визначає вибір порядку методу.
3. Встановлюється нове значення часового кроку на основі заданої користувачем похибки розв'язку є (8.56) з урахуванням обраного прогнозованого мінімального значення локальної похибки Ei(10.50) і залежності похибки розв'язку від порядку методу k(8.9):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.