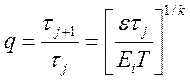Оцінка локальної похибки і організація обчислень, страница 2

                                                                                                     (10.51)

де— задана користувачем відносна похибка обчислень, Т — часовий ін­тервал розв'язку,— попередній крок.

10.8.2. Алгоритм з обмеженим вибором порядку методу

Застосовується у випадках, коли використовуються формули методів Гіра змін­ного порядку і змінного кроку (10.22) і (10.27), а похибка визначається через різницю прогнозованого і обчисленого значень (10.47). Цей алгоритм передба­чає виконання таких кроків.

1. Прогнозуються похибки для трьох методів із різними порядками точності:

        

Після kкроків порядок методу змінюється відповідно до значення, що за­безпечує мінімальну похибку

2. Обчислюється новий крок за формулою (10.51).

Більшу функціональну гнучкість першого алгоритму порівняно з другим за­безпечує зменшення кількості кроків на заданому інтервалі розв'язку і можли­вість досить стійкого керування обчисленнями.

Нагадаємо, що коефіцієнти формул наближення методів змінного порядку і змінного кроку обчислюються на кожному кроці за формулами (10.23), (10.25), (10.28) і (10.31), що збільшує обсяг обчислень. Тому була запропонована спро­щена схема організації обчислень зі змінним кроком, коли використовуються формули наближення з постійними коефіцієнтами, які перераховуються з ви­користанням інтерполяційних поліномів, побудованих на основі раніше обчис­лених значень. Це досягається збереженням попередніх значень у вигляді век­тора скінчених різниць вищих порядків

                                       (10.52)

або вектора Нордсика

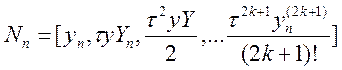
                                                                             (10.53)

У першому випадку старі й нові значення пов'язані через коефіцієнт q, обу­мовлений виразом (10.51):

          

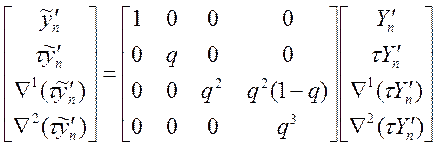
або в матрично-векторній формі

                                                                                                              (10.54)

У другому випадку для вектора Нордсика обчислення збережених значень для нового значення кроку спрощується:

                                                                                                           (10.55)

тому що матриця обчислення значень на відміну від матриці є чис-

то діагональноюненульові елементи в ній визначаються коефі-

цієнтом qв i-му степені.

10.9. Об'єднаніявно-неявніпроцедури

Як відзначалося вище, неявні методи ефективно використовуються для моде­лювання динамічних процесів у широкосмугових інформаційних системах, ос­кільки автоматичний вибір їх порядку і кроку визначається характером розв'язку. На рис. 10.7 показана типова перехідна характеристика системи, на якій можна чітко виділити дві ділянки: швидко наростаючий передній фронт, на якому об­числення виконуються з малим кроком, і згасаючий процес, де крок обчислень істотно збільшується через повільну зміну значень змінної.

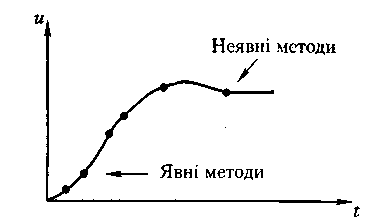
Рис. 10.7. Типова перехідна характеристика з виділеними ділянками використання явних і неявних методів

Тому доцільно побудувати такі об'єднані явно-неявні процедури, у яких на ділянках швидкої зміни розв'язку обчислення виконувалися б за допомогою яв­них методів, а на ділянках повільної зміни розв'язку (малоінформативні) — за допомогою неявних методів, які дозволяють довільно змінювати (і збільшувати) крок. У таких процедурах необхідно автоматично розпізнавати ділянки розв'яз­ку і автоматично вибирати відповідний метод розв'язування.

Одним із можливих шляхів розпізнавання локальної «жорсткості» розв'язку в околі точки   є перевірка виконання умови