Информатика и выч. техника \ Численные методы в информатике

Оцінка локальної похибки і організація обчислень, страница 4

Явний нелінійний метод Федули першого порядку                                                                    0,150047

Неявний метод BDF п'ятого порядку                                                                                        0,156484

Як свідчать дані табл. 10.2, явний нелінійний метод Федули більш точний, ніж неявний ме­тод Ейлера. У разі розв'язування нелінійного рівняння його точність наближається до точ­ності неявних методів другого порядку.

10.10.2. Явний нелінійний метод другого порядку

Існує явна формула Глинського другого порядку для розв'язання жорсткого ди­ференціального рівняння:

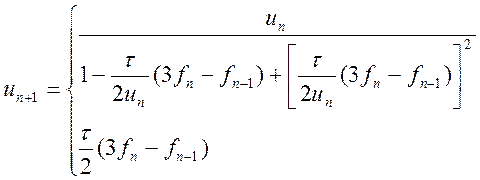якщо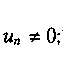

                                                                                                якщо

             (10.63)                                                          

Стійкість цієї формули можна довести, розглядаючи дві сусідні ітерації, на яких для модельного рівняннямає виконуватися така умова:

                                                       (10.64)

Використовуючи модельне рівняння, перетворимо вираз (10.63):

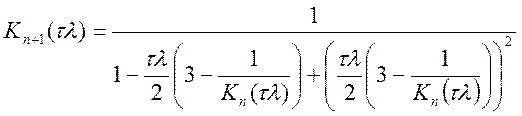                              (10.65)

Проаналізувавши знаменник формули (10.65), переконаємося:

♦  якщото  і умова (10.64) виконується;

♦  якщо то і умова (10.64) все ж виконується;

♦  якщо   то, коли досягається мінімаль­не значення знаменника виразу (10.65), рівне 3/4, у результаті чого    і умова (10.64), як і раніше, виконується.

Приклад 10.7

Розв'яжіть систему рівнянь

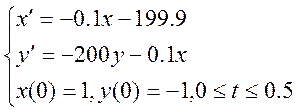
методом Глинського в разі обчислень із кроком

Неважко бачити, що власні значення матриці Якобі відповідно          Тому за обраного кроку явні методи не забезпечують збіжності розв'язку цієї системи, ос­кільки згідно з виразом (10.2) коефіцієнт жорсткості Пакет Mathematica дозволяє знайти точний розв'язок системи диференціальних рівнянь за допомогою оператора DSolve:

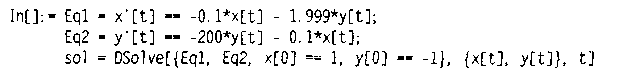
Отримаємо розв'язок у вигляді:

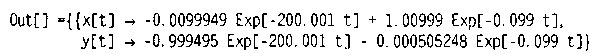
і обчислимо значення змінних для двох моментів часу (табл.10.3):

 Таблиця 10.3. Результати оцінки точних значень змінних

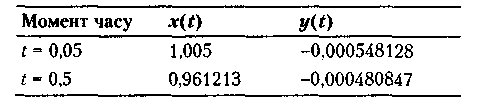
Враховуючи початкове значення  y(0) = -1,  на основі даних таблиці робимо висновок, що вже протягом першого кроку t= 0,05 «швидка» змінна y(t) зменшується майже до нуля, в той час як «повільна» змінна х(t) майже не змінюється. Програмна реалізація методу Глинського в пакеті Mathematica набуває такого вигляду:

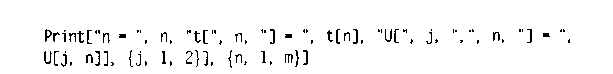
Отримані результати зведені в табл. 10.4.

Таблиця 10.4. Оцінки значень змінних

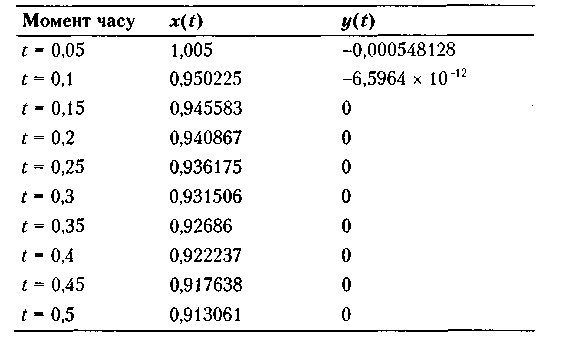
Результати в таблиці свідчать про те, що коли явні лінійній методи зовсім непрацездат­ні, явний нелінійний метод Глинського працює бездоганно і забезпечує збіжність роз­в'язку, хоча й з невеликою точністю (кілька відсотків) через високе значення вибраного кроку.

На жаль, спроби побудувати явні нелінійні методи більш високого порядку не дали вра­жаючих результатів, оскільки необхідний для них обсяг обчислень перевищує той, що потрібний для реалізації звичайних неявних методів, розглянутих у цьому розділі.

10.11. Засобирозв'язанняжорсткихзадач упакетіMathematica

У пакеті Mathematica існує можливість настроїти стандартну операцію NDSolve на використання неявних методів BDF Брайтона (10.27) і (10.28) з автома­тично змінюваними порядком методу — від першого до п'ятого — і кроком об­числення. Наприклад, розв'язання задачі з прикладу 10.4 , to=0, y0=1 в інтервалі [0, 0,5] і знаходження значення у(0,4) виконується у такий спосіб:

Це значеннябуло використане раніше в табл. 10.2.

  Знайдемо також розв'язок жорсткої задачі з прикладу 10.5:

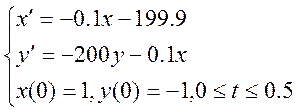
методом BDF і знайдемо значення x(0,5) і y(0,5).

Для цього запишемо і виконаємо таку послідовність операцій:

Скачать файл