
Знайдемо значення х(0,5) і y(0,5).
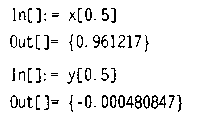
Отримані значення ![]() з
точністю 10~6
з
точністю 10~6
збігаються з точними значеннями x*(0.5)=0.961213 і y*(0.5)=-0.000480847
наведеними в табл.10.3.
Розробники пакета Mathematica передбачили в разі використання стандартного оператора NDSolve можливість автоматичного переходу від явних методів Адамса (від першого до дванадцятого порядку) до неявних методів BDF (від першого до п'ятого порядку) і навпаки. Це досягається за допомогою оператора NDSolve без вказівки на необхідний метод чи введенням у формат оператора опції Method -> Automatic. Тобто під час виконання оператора NDSolve відповідна програма, яка досить велика (на мові Mathematica вона містила б кілька тисяч рядків коду!) спочатку аналізує жорсткість задачі, а потім на основі оцінки жорсткості приймається рішення щодо використання явного чи неявного методу. Значення кроку і порядок методу змінюється, виходячи з умови забезпечення потрібної точності (див. підрозділ 10.8). Результати обчислень зі змінними кроком і порядком потім використовуються для побудови інтерполяційного полінома Лагранжа чи Ерміта (оператор InterpolatingFunction), за допомогою якого будуються відповідні таблиці та графіки.
Однак спільні явно-неявні процедури, розглянуті в підрозділі 10.9, під час розв'язання однієї й тієї ж самої задачі в пакеті Mathematica поки що не реалізовані.
Висновки
1. Моделями широкосмугових імпульсних систем є переважно жорсткі системи диференціальних рівнянь, шо визначає для їх розв'язання пріоритетне використання неявних методів.
2. Серед існуючих неявних методів найбільш ефективними з погляду мінімізації кількості кроків на заданому інтервалі (і як наслідок зменшення обсягу обчислень) є неявні методи змінного порядку і змінного кроку BDF і Гіра, які зберігають стійкість до шостого порядку включно. Ці методи передбачають зміну коефіцієнтів формул після кожної зміни значення кроку чи порядку методу. Процедура зміни порядку і кроку за заданими користувачем загальною похибкою і загальним часом обчислення у таких методах виконується автоматично.
3. Автоматична процедура вибору порядку методу і кроку враховує неоднаковий ступінь стійкості неявних методів різного порядку, яка залежить від А -стійкості, властивої неявним методам першого і другого порядків, і Л(а)-стійкості, характерної для методів третього-шостого порядків.
4. Для моделювання автоколивальних систем зі змінною частотою, в яких власні значення матриць Якобі розташовані на уявній осі комплексної площини, рекомендується використовувати неявні методи першого і другого порядків, області стійкості яких включають уявну вісь.
5. Можлива модифікація автоматичної процедури зміни кроку і порядку методу, яка передбачає використання методів з постійними коефіцієнтами, але з обов'язковим перерахунком інтерполяційних поліномів, побудованим на основі збережених значень коефіцієнтів.
6. Під час розв'язання жорстких задач перспективним є використання явно-неявних процедур, які забезпечують автоматичний перехід від явного методу до неявного (і навпаки), в залежності від поточних результатів обчислень.
Контрольнізапитаннятазавдання
1. Розв'яжіть неявним методом Гіра третього порядку (10.19) рівняння
2. ![]()
![]() яке
було розв'язане раніше, в прикладі 10.1, неявним
яке
було розв'язане раніше, в прикладі 10.1, неявним
методом Ейлера. Необхідно, як і раніше, з
кроком ![]() знайти
значення y(0,2).
знайти
значення y(0,2).
2. Найдіть
умови стійкості формули наближення методу середньої точки
![]() для випадку
для випадку![]()
3. Визначіть,
чи є серед наведених різницевих рівнянь такі, що забезпечують
стійкі розв'язки:
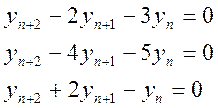
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.