ЛАБОРАТОРНАЯ РАБОТА № 3 (5-1)
Приближенное решение уравнения f(x)=0 методом Ньютона
Составить и отладить программу на языке Си, реализующую метод Ньютона для решения уравнения общего вида, с произвольной функцией, имеющей на [a;b] корень.
Метод Ньютона для решения уравнений вида (1) для произвольной функции f(x) состоит в построении итерационной последовательности:
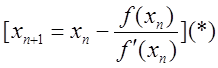 |
сходящейся при n→∞ к корню уравнения.
Метод эффективно применим, если подобрано хорошее начальное приближение xo и гарантирует высокую скорость сходимости.
Теорема: (Достаточные условия сходимости).
Пусть функция f(x) определена и дважды непрерывно дифференцируема, причем производные f’(x) и f’’(x) сохраняют знаки на отрезке [a,b] (т.е. на этом отрезке есть корень),
тогда исходя из начального приближения xo , удовлетворяющего условию
f(xo)*f’’(xo)>0 итерационный процесс (*) сходится к единственному на [a,b] корню ξ : f(ξ)=0, ξ Î [a,b].
#include "stdafx.h"
#include <conio.h>
#include <math.h>
const float a=2.113f;
const float b=-6.44f;
const float c=-3.19f;
const float d=15.13f;
const float m=2.41064f; const float M=20.0828f;
float f (float);
float df (float);
int main(int argc, char* argv[])
{
float x0,xk,a,b,epsilon;
printf("Нахождение корня функции f(x) = 0 с начальным приближением x0 \nметодом Ньютона\n");
printf("Вычисления производятся для функции f(x)=ax^3+bx^2+cx+d, при \na=2.113\nb=-6.44\nc=-3.19\nd=15.13\n");
printf("Левая граница отрезка: ");
scanf("%f",&a);
printf("Правая граница отрезка: ");
scanf("%f",&b);
printf("Начальное приближение: ");
scanf("%f",&x0);
printf("Точность вычислений: ");
scanf("%f",&epsilon);
xk=x0;
do
{
x0=xk;
xk=x0-(f(x0)/df(x0));
}
while (fabs(xk-x0)>sqrt(fabs(2.f*epsilon*m/M)));
printf("Значение корня: %f\n",x0);
getch();
return 0;
}
float f (float x)
{
return (a*x*x*x + b*x*x + c*x + d);
}
float df (float x)
{
return (3*a*x*x + 2*b*x + c);
}
Рассмотрим тестовый пример, решение которого может быть легко найдено аналитически.
y(x) = (x-1)(x+1)
Рассмотрим отрезок [0.6, 1.6]
Поведение функции, ее первой и второй производных на этом отрезке:
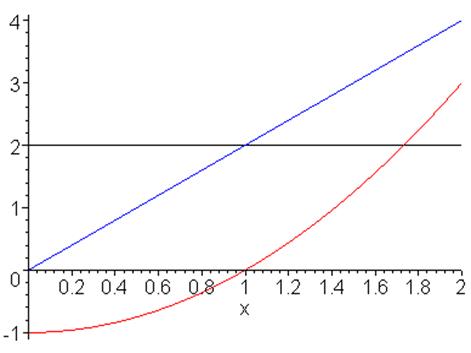
Рассмотрим ![]() и
и![]() на этом
отрезке
на этом
отрезке
![]() = 2x
= 2x![]() = 2
= 2
Итак, величина
![]()
А величина:
равна 2.
Тогда, при выбранной точности 0.00001 для
окончания итерационного процесса следует использовать ![]()
![]()
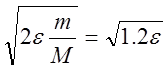
Результаты работы программы:
Левая граница отрезка: 0.6
Правая граница отрезка: 1.6
Начальное приближение: 0.6
Точность вычислений: 0.00001
Значение корня: 1.000031
Для функции вида:
![]()
a=2.113, b= -6.44, c= -3.19, d= 15.13;
Выберем отрезок, на котором заданная функция имеет ровно один корень.
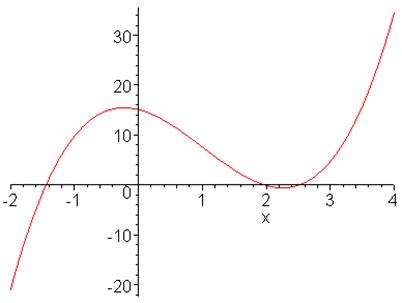
Это отрезок [2.4 , 2.6]
Рассмотрим первую и вторую производные заданной функции на этом отрезке, для выбора величин M и m.
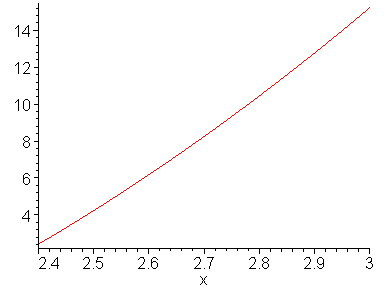
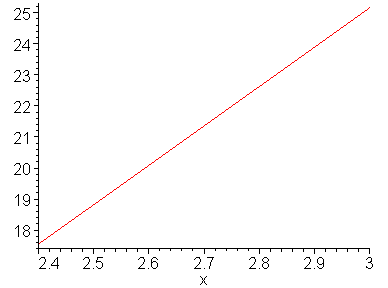
Аналитическое представление второй производной: 12.678x – 12.88
Аналитическое представление первой производной: 6.339x2 – 12.88x – 3.19
m = 2.41064
M= 20.0828
Новая величина точности будет равна: .1549419600e-2
Результат работы программы:
Левая граница отрезка: 2.4
Правая граница отрезка: 2.6
Начальное приближение: 2.4
Точность вычислений: 0.00001
Значение корня: 2.518090
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.