ЛАБОРАТОРНАЯ РАБОТА № 5 (1-1)
Решение системы нелинейных уравнений методом Ньютона
Рассмотрим общий случай – решение системы n нелинейных уравнений с n неизвестными
F(x)=0,
где ![]() ,
, ![]()
Будем предполагать отображение ![]() непрерывно
дифференцируемо в некоторой окрестности решения z, так что
непрерывно
дифференцируемо в некоторой окрестности решения z, так что 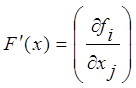
Обозначим 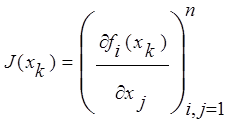
![]() - матрица Якоби системы в точке
- матрица Якоби системы в точке ![]() .
.
Вообще говоря, метод решения системы нелинейных уравнений имеет много общего с методом решения одного нелинейного уравнения. В случае одного нелинейного уравнения метод Ньютона аппроксимирует его линейным уравнением, полученным использованием первых двух членов ряда Тейлора. Так же можно поступить и в случае системы n уравнений.
Пусть ![]() - текущее приближение к
решению z системы F(x)=0. Тогда в
точке
- текущее приближение к
решению z системы F(x)=0. Тогда в
точке ![]() можно записать разложение в ряд Тейлора:
можно записать разложение в ряд Тейлора: ![]()
Рассмотри первые два члена ряда Тейлора.
Получаем аппроксимацию нелинейных функций: ![]()
![]()
Для определения следующего приближения ![]() к решению будем использовать нуль линейной
аппроксимации, то есть положим нулю правую часть нашего равенства; получим
систему линейных уравнений:
к решению будем использовать нуль линейной
аппроксимации, то есть положим нулю правую часть нашего равенства; получим
систему линейных уравнений: ![]() ; или
; или ![]()
Эту систему можно решить при помощи метода Гаусса. Из
этой системы находим p, а новое приближение к решению получаем по формуле ![]() , то есть
, то есть
![]() - формула метода
Ньютона.
- формула метода
Ньютона.
Обозначим ![]() . Пусть при некоторых
. Пусть при некоторых ![]() , выполняются условия:
, выполняются условия:
1) ![]() при
при ![]()
2) ![]() при
при ![]()
Обозначим также ![]() ,
, ![]() ,
, ![]() -
евклидова норма в
-
евклидова норма в ![]()
Теорема (о сходимости метода Ньютона)
При
условиях 1), 2) и ![]() итерационный процесс Ньютона
сходится с оценкой погрешности
итерационный процесс Ньютона
сходится с оценкой погрешности ![]()
#include "stdafx.h"
#include <math.h>
#include <conio.h>
// Количество уравнений
const n = 2;
void GaussSolve (float a[n][n],float b[n],float x[n]);
float Norm (float x[n]);
float f1(float x[n]);
float f2(float x[n]);
float df1_dx(float x[n]);
float df1_dy(float x[n]);
float df2_dx(float x[n]);
float df2_dy(float x[n]);
typedef float (*lpFunction)(float* f);
const float a = 1.0f;
const float b = 7.5f;
int main(int argc, char* argv[])
{
int i,j, iter=0;
// Точность
float eps = 1e-5;
printf ("%s","Решение системы нелинейных уравнений методом Ньютона\n");
printf ("Точность вычислений: %f\n",eps);
// Матрица
float a[n][n];
// Вектор правых частей
float b[n];
// Вектор решения
float x[n], xk[n],p[n];
lpFunction Jacobi[n][n];
Jacobi[0][0] = df1_dx; Jacobi[0][1] = df1_dy;
Jacobi[1][0] = df2_dx; Jacobi[1][1] = df2_dy;
// Выбираем начальное приближение
xk[0]=1.5;xk[1]=7;
do
{
iter++;
for (i=0;i<n;i++)
{
x[i] = xk[i];
}
// Заполняем матрицу A
for (i=0;i<n;i++)
for (j=0;j<n;j++)
{
a[i][j] = Jacobi[i][j](x);
};
// Заполняем вектор правых частей
b[0]=-f1(x); b[1]=-f2(x);
GaussSolve (a,b,p);
// Получаем следующее приближение, складывая предыдущее и вновь полученное
for (i=0;i<n;i++)
{
xk[i] = x[i] + p[i];
}
}
while (fabs(Norm (x) - Norm(xk))>=eps);
printf ("%s","Вектор решения: [ ");
for (i=0;i<n;i++)
{
printf ("%f ",xk[i]);
}
printf ("%s","]\n");
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.