Міністерство освіти і науки України
Сумський державний університет
Кафедра Інформатики
Секція ІТП
Звіт по лабораторній роботі № 4
Тема: Обчислення власних значень і власних векторів матриці
Виконала: студентка групи ІТ-72
Шулима Ольга
Перевірив: Неня В.Г.
Суми 2009
1. Знайти власні значення матриці з прикладу:
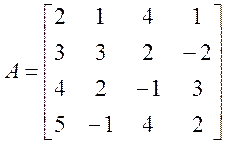 |
Іn[]:=A={{2, 1, 4, 1}, {3, 3, 2, -2}, {4,2,-1,3}, {5, -1, 4, 2}}
0ut[]= {{2,1,4,1},{3,3,2,-2},{4,2,-1,3},{5,-1,4,2}}
Іn[]:=Eigenvalues[A]
0ut[]={7.98285, 4.16393, -4.08441, -2.06237},
Матриця А має чотири дійсні власні значення.
Команда Eigenvalues[A] знаходить власні значення матриці.
2. Знайти, користуючись QR-алгоритмом з перетворенням Хаусхолдера, власні значення матриці

SchurDecomposition[A] поле розкладу Хаусхолдера для числової матриці А. Результат – список {q, r}, де q – ортогональна матриця і r – верхня трикутна матриця.
Висновки: У ході виконання лабораторної роботи ми розглянули, як обчислювати власні значення, власні вектори матриці.
У пакеті Mathematica реалізовано метод характеристичного рівняння матриці det(A-λЕ)=P(λ)=0, який для початкової матриці А запускається такими командами:
Eigenvalues [А] —для обчислення власних значень;
Eigenvectors [А] —для обчислення власних векторів;
Eigensystem [A] — для одночасного визначення власних значень і векторів матриці.
Тестові питання до лабораторної роботи № 4
Тема: Обчислення власних значень і власних векторів матриці
1. Що знаходять за допомогою команди SchurDecomposition[A]?
А) Власні значення матриці А.
Б) поле розкладу Хаусхолдера для числової матриці А.
В) Одночасно і власні значення, і власні вектори матриці А.
2. У пакеті Mathematica реалізовано QR-алгоритм, що базується на перетворенні Хаусхолдера. Яким стандартним оператором викликається цей алгоритм?
А) CharacteristicPolynomial[A,х].
Б) SchurDecomposition[A].
В) Eigensystem [A].
3. Що означає команда MatrixForm?
А) Подання матриці у табличній формі за допомогою стовпців та рядків:
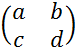
Б) Запис матриці в одному рядку {{a,b}, {c,d}}
В) Зміна попередньої форми запису матриці на протилежну, тобто з табличної форми у рядкову та навпаки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.