ЛАБОРАТОРНАЯ РАБОТА № 1 (1-3)
Приближенное решение уравнения f(x)=0, методом деления пополам (метод бисекции)
1. Постановка
задачи.
Составить и отладить программу на языке Си,
реализующую метод бисекции для произвольной функции, имеющей на отрезке [a,b] корень
по теореме Больцано-Коши.
2. Теоретическое обоснование метода
Если функция f(x) на концах принимает значения разных знаков: f(a)*f(b)<0, то тогда $ такое значение x=c, что f(c)=0; cÎ[a,b], причем корень будет единственен, если производная на рассматриваемом интервале не меняет знака.
3. Алгоритм решения
·
Получаем границы отрезка ![]() и требуемую точность вычислений
и требуемую точность вычислений
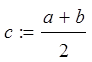
4. Текст программы
#include "stdafx.h"
#include <math.h>
#include <conio.h>
#define FALSE 0
#define TRUE 1
// Tested with params
// [4;5]
// 0.00001
float f (float);
int main(int argc, char* argv[])
{
float a,b,c,epsilon;
char blnError = FALSE;
printf("Нахождение корня функции f(x) = 0 на отрезке [n1,n2] \nметодом деления пополам (бисекции)\n");
printf("Вычисления производятся для функции f(x)=tg(ax)-bx, \nпри a=0.9464 и b=1.3825\n");
printf("Введите границы отрезка для нахождения корня\n");
printf("Левая граница отрезка: "); scanf("%f",&a);
printf("Правая граница отрезка: "); scanf("%f",&b);
printf("Точность вычислений: "); scanf("%f",&epsilon);
do
{
c=(a+b)/2;
((f(c)*f(a)<0)?b:a)=c;
if (f(c)==0)
{
printf ("Значение функции в точке %f равно нулю\n",c);
blnError = (f(c-epsilon/2)*f(c+epsilon/2)<0)?FALSE:TRUE;
break;
}
}
while (fabs(f(c))>epsilon || fabs(b-a)>epsilon);
if (blnError)
{
printf ("Однако, на концах отрезка [%f-%f,%f+%f] \nфункция не принимает значения разных знаков\n",c,epsilon,c,epsilon);
}
else
{
printf("Значение корня: %f\n",c);
}
getch();
return 0;
}
float f (float x)
{
const float a = 0.9464; const float b = 1.3825;
return tan(a*x)-b*x;
};
5. Тестовый
пример
Рассмотрим работу программы на тестовом примере, решение которого известно:
Уравнение: (x-1)(x+1) = 0
Решение: x=3; y=-1
а)
Левая граница отрезка: -2
Правая граница отрезка: 2
Точность вычислений: 0.0001
Значение функции в точке -1.000000 равно нулю
Значение корня: -1.000000
б)
Левая граница отрезка: 0
Правая граница отрезка: 3
Точность вычислений: 0.00001
Значение корня: 1.000002
Уравнение: tg (ax) – bx = 0 a=0.9464, b=1.3825
На
отрезке -![]() функция
имеет вид:
функция
имеет вид:
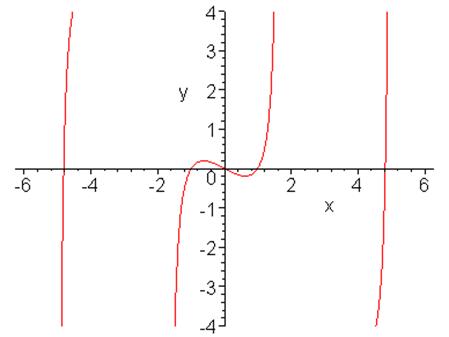
Рассмотрим интервал [0.5, 1.5], на котором функция удовлетворяет условиям Больцано-Коши.
Результат работы программы:
Левая граница отрезка: 0.5
Правая граница отрезка: 1.5
Точность вычислений: 0.00001
Значение корня: 0.996147
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.