Решение системы линейных уравнений методом Гаусса (Лабораторная работа № 4 (13))

ЛАБОРАТОРНАЯ РАБОТА № 4 (13)

Решение системы линейных уравнений методом Гаусса

1. Постановка задачи.
    

Составить и отладить программу на языке Си, реализующую метод Гаусса для произвольной системы линейных уравнений.

2. Алгоритм решения

Рассмотрим систему линейных алгебраических уравнений:

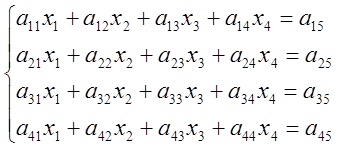Шаг 1. Полагаем a11≠ 0. Если это не так, то переставим соответствующим образом строки.

Умножаем 1-е уравнение на (1/a11) , получаем:

(1)

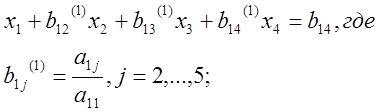Шаг 2.  Исключаем  x1 из всех последующих уравнений, умножаем (1) на a21 и вычитаем из второго уравнения первое, получим уравнение:

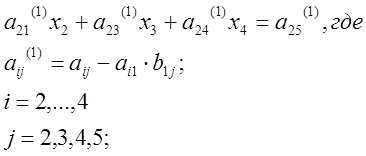(2)

И так поступаем со всеми уравнениями;

Получим матрицу размерности на единицу меньше:

Шаг 3. Предполагаем:

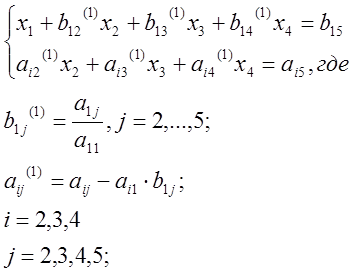делим уравнение (2) на этот элемент, получаем:

имеем систему: 

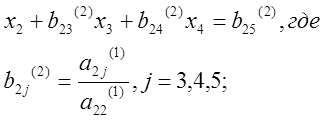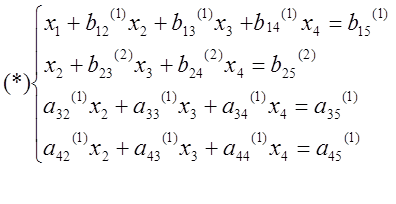Шаг 4.  

Исключаем x1 из всех последующих, умножаем второе уравнение системы (*) на элемент   

и вычитаем его из соответствующего j-го уравнения, в результате имеем систему:

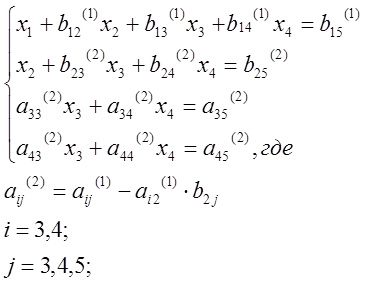Шаг 5.  

В предположении, что коэффициент при x3 ненулевой (если это не так, то переставим строки системы), делим на него третье уравнение, получаем:

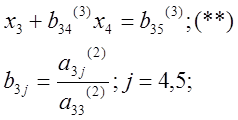Шаг 6.

Исключаем из последующих (-его) уравнения x3 ,  умножаем уравнение (**) на элемент

и вычитаем его из j-го уравнения, в результате имеем систему:

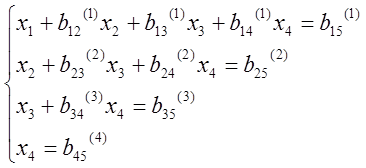Вместо исходной системы получаем систему с верхнетреугольной матрицей:

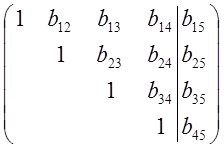Это называется прямым ходом метода.

1.2. Обратный ход:

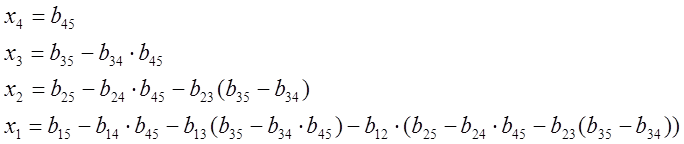В общем виде решение системы с верхнетреугольной матрицей С:

Cx=y, есть:

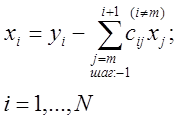N – число уравнений;

Или же можно в следующем виде:

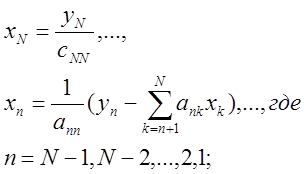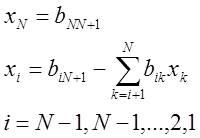
В нашем случае ann (bnn) = 1, получаем:

3. Текст программы

#include "stdafx.h"

#include <math.h>

#include <conio.h>

int main(int argc, char* argv[])

{

                  const float eps=0.0001f;

                  const n=3;

                  float tmpValue;

                  int i,j,k,z;

                  float dblLeadElement;

                  float a[n][n];

                  float b[n];

                  float x[n];

                  a[0][0]=3.72f;  a[0][1]=3.47f;  a[0][2]=3.06f;

      a[1][0]=4.47f;  a[1][1]=4.1f;   a[1][2]=3.63f;

      a[2][0]=4.96f;  a[2][1]=4.53f;  a[2][2]=4.01f;

      b[0]=30.74f;    b[1]=36.8f;     b[2]=40.79f;

                  int w,q;

                  printf ("%s","Расширенная матрица системы имеет вид: \n");

                                    for(w=0; w<n; w++)

                                                      {

                                                          for(q=0; q<n; q++)

                                                                        {

                                                                                          printf ("%f  ",a[w][q]);

                                                                        }

                                                                        printf ("%f  \n",b[w]);

                                                      }

                                      printf ("\n");

                  for(i=0; i<n; i++)

                  {

                                      dblLeadElement=a[i][i];

                                      float tmpMax = dblLeadElement;

                                      int tmpMaxNumber = i;

                                      for (z=i;z<n;z++)

                                      {

                                                        if (a[z][i]>tmpMax){tmpMax = a[z][i];tmpMaxNumber=z;}

                                      }

                                      for (z=i;z<n;z++)

                                      {

                                                        tmpValue = a[i][z];

                                                        a[i][z] = a[tmpMaxNumber][z];

                                                        a[tmpMaxNumber][z] = tmpValue;

                                      }

                                      tmpValue = b[i];

                                      b[i] = b[tmpMaxNumber];

                                      b[tmpMaxNumber] = tmpValue;

                                      dblLeadElement = tmpMax;

                                      for(j=i; j<n; j++)

                                                      {

                                                                        a[i][j]/=dblLeadElement;

                                                      }

                                                      b[i]/=dblLeadElement;

                                      for(k=i+1; k<n; k++)

                                                      {

                                                          float dblToDivide=a[k][i]/a[i][i];

                                                                        for(z=i;z<n; z++)

                                                                        {

                                                                            a[k][z]-=a[i][z]*dblToDivide;

                                                                        }                                 

                                                                        b[k]-=b[i]*dblToDivide;

                                                      }

                  }

                  x[n-1]=b[n-1];

    for(k=n-2; k>=0; k--)

                  {

                    float sum=b[k];

                    for(j=k+1; j<n; j++)

                                    {

                                                      sum-=a[k][j]*x[j];

                                    }

      x[k]=sum;

                  }

                  printf ("x=[ ");

                  for (i=0;i<n;i++){printf ("%f ",x[i]);};

                  printf ("]\n");

                  return 1;

}

4. Расчетный пример

Результат работы программы:

Расширенная матрица системы имеет вид:

3.720000  3.470000  3.060000  30.740000

4.470000  4.100000  3.630000  36.799999

4.960000  4.530000  4.010000  40.790001

x=[ 6.195108 1.194872 1.159474 ]