Сумський Державний Університет
по дисципліні
“Теорія ймовірностей та математична статистика”
(п’ятий семестр)
Модуль 2
Суми – 2010
Завдання по дисципліні “Теорія ймовірностей і математична статистика” для студентів механіко-математичного факультету очної форми навчання – Модуль 2.
Укладач – проф. Мазманішвілі О.С., професор кафедри моделювання складних систем.
Затверджено на засіданні кафедри моделювання складних систем СумДУ (протокол № 8 от 28.05.2010 г.)
ЗАДАЧА 1 (ДЛЯ ВСІХ ВАРІАНТІВ)
Отримана вибірка
об’єму ![]() :
:
7, 1, 4+m,
3, 2+k, 16+2![]() , 15+n, 4, 1, 1, 3+k, 5,
, 15+n, 4, 1, 1, 3+k, 5,
5, 6, 6, 6, 1, 5+m, 3+n, 14+2m, 2, 2, 7, 7, 7, 4, 4,
3, 1, 2+p, 6, 8, 4, 15+3p, 1+k, 1+m, 1+n, 5, 5, 3.
В задачі потрібно:
1. Побудувати: інтервальний варіаційний ряд розподілу; гістограму; емпіричну функцію розподілу.
2. Знайти: вибіркове середнє, вибіркову дисперсію, середнє квадратичне відхилення, медіану і моду вибірки.
3. Оформити результати графічно.
Розрахункова таблиця для визначення варіанту роботи до Задачі 1
Номер варіанта Параметри
1 k = 2, m = 5, n = 1, p = 5.
2 k = 3, m = 2, n = 6, p = 2.
3 k = 2, m = 3, n = 1, p = 1.
4 k = 6, m = 3, n = 2, p = 3.
5 k = 1, m = 7, n = 3, p = 2.
6 k = 1, m = 2, n = 7, p = 3.
7 k = 1, m = 1, n = 2, p = 0.
8 k = 3, m = 1, n = 2, p = 1.
9 k = 1, m = 2, n = 3, p = 1.
10 k = 8, m = 2, n = 3, p = 1.
11 k = 8, m = 5, n = 2, p = 2.
12 k = 1 m = 3, n = 2, p = 2.
13 k = 2, m = 1, n = 2, p = 1.
14 k = 3, m = 2, n = 1, p = 2.
15 k = 4, m = 3, n = 2, p = 3.
16 k = 1, m = 4, n = 1, p = 2.
17 k = 2, m = 4, n = 3, p = 4.
18 k = 2, m = 1, n = 1, p = 3.
19 k = 2, m = 3, n = 1, p = 4.
20 k = 4, m = 2, n = 3, p = 1.
21 k = 2, m = 2, n = 3, p = 2.
22 k = 2, m = 3, n = 4, p = 2.
23 k = 1, m = 1, n = 4, p = 2.
24 k = 2, m = 4, n = 3, p = 3.
25 k = 3, m = 1, n = 3, p = 3.
26 k = 3, m = 2, n = 1, p = 2.
ЗАДАЧА 2 (ДЛЯ ВСІХ ВАРІАНТІВ)
1. Випадкова величина Х задана густиною розподілу ймовірностей:
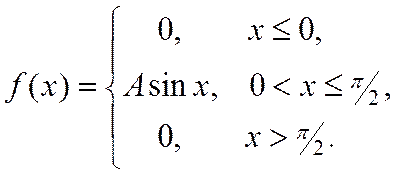
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
2. Випадкова величина Х задана густиною розподілу ймовірностей:
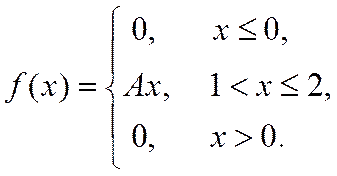
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
3. Випадкова величина Х задана густиною розподілу ймовірностей:
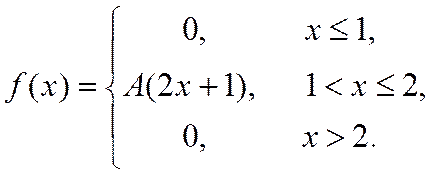
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
4. Випадкова величина Х задана густиною розподілу ймовірностей:
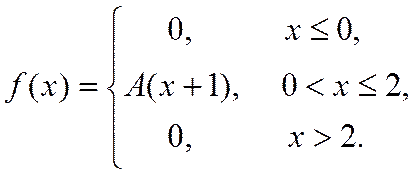
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
5. Випадкова величина Х задана густиною розподілу ймовірностей:
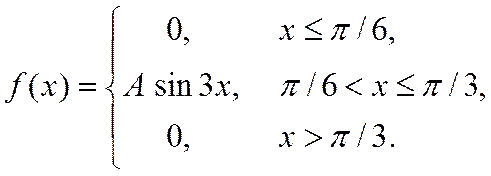
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
6. Випадкова величина Х задана густиною розподілу ймовірностей:
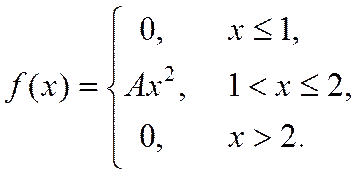
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
7. Випадкова величина Х задана густиною розподілу ймовірностей:
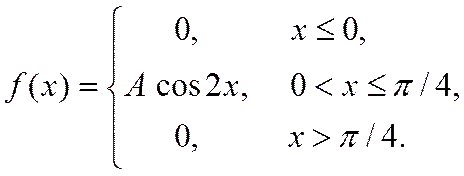
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
8. Випадкова величина Х задана густиною розподілу ймовірностей:
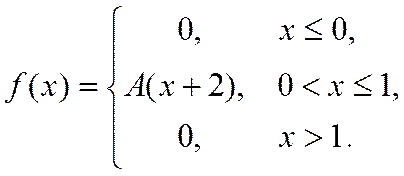
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
9. Випадкова величина Х задана густиною розподілу ймовірностей:
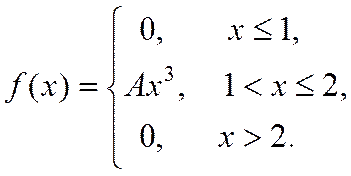
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
10. Випадкова величина Х задана густиною розподілу ймовірностей:
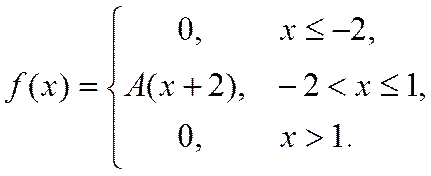
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
11. Випадкова величина Х задана густиною розподілу ймовірностей:
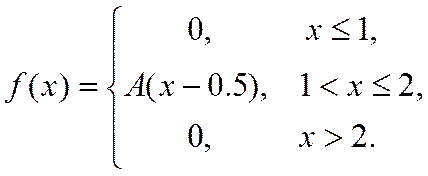
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.