Завдання по дисципліні “Теорія ймовірностей і математична статистика” для студентів механіко-математичного факультету. Модуль 2, страница 6

Задача  11

Знайти характеристичну функцію гіпергеометричного закону розподілу.

Задача 12

На глобусі випадково обрана точка.

Знайти ймовірність наступних подій:

a) координати точки знаходяться між 90-м і 180-м градусами східної довготи;

б) координати точки знаходяться між 45-м і 90-м градусами північної широти;

в) координати точки знаходяться між 90-м і 180-м градусами східної довготи, а також між 45-м і 90-м градусами північної широти.

Оформити результат графічно.

Задача 13

Система незалежних випадкових величин (,,,,,) має нормальну густину з нульовим математичним очікуванням і одиничною дисперсією кожна.

Знайти густину розподілу наступної комбінації цих величин:  Y=+++++. Оформити результат графічно.

Задача 14

Розглядається система випадкових величин (X,Y,Z). Вона має густину розподілу

,   .

Знайти густину розподілу суми S=X+Y+Z. Оформити результат графічно.

Задача  15

Система з двох випадкових величин (X,Y) має сумісну густину .

Знайти густину розподілу  мінімальної з цих двох величин  Z=min(X,Y). Оформити результат графічно.

Задача 16

Випадкові величини X і Y визначені на всій числовій оси та мають густину розподілу

,  .

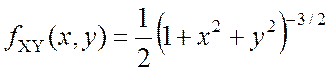Знайти густину розподілу випадкової величини Z=X+Y. Оформити результат графічно.

Задача 17

Випадкова величина X має густину розподілу ймовірностей 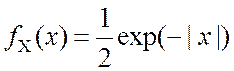 ,  ;  незалежна від неї випадкова величина Y розподілена так же.

Знайти закон розподілу композиції Z=X+Y. Оформити результат графічно.

Задача 18

Найти закон розподілу композиції Z=X+Y двох незалежних випадкових величин X и Y, розподілених за законом Коші. Оформити результат графічно.

Задача 19

Випадкова величина X має густину розподілу ймовірностей  , ; незалежна від неї випадкова величина Y має такий же закон розподілу.

Знайти густину розподілу відношення Z=X/Y. Оформити результат графічно.

Задача 20

Відрізок довжиною L обертається в прострілі таким чином, що всі його можливі орієнтації рівноправні.

Знайти закон розподілу довжини проекції цього відрізка на виділену площину. Оформити результат графічно.

Задача 21

Система випадкових величин (X,Y) має густину розподілу ,  .

Знайти густину розподілу  випадкової величини Z, яка є одним з розв’язків рівняння  Z+2(X/Y)Z–1=0. Оформити результат графічно.

Задача 22

Випадкові величини X і Y описуються нормальними законами з параметрами (,) і (,) відповідно.

Знайти закон розподілу випадкової величини Z=X/Y, Оформити результат графічно.

Задача 23

На площині заданий відрізок довжиною L, який обертається випадковим образом так, що всі напрями його однаково ймовірні.

Визначити математичне очікування і дисперсію випадкової довжини проекції відрізка на вісь абсцис.

Задача 24

Сумісна густина розподілу ймовірностей випадкових величин (X,Y) наступна

,       .

Знайти: коефіцієнт , закон розподілу випадкової величини U=X+Y. Оформити результат графічно.

Задача 25

Система незалежних випадкових величин (,,) має нормальну густину з нульовим математичним очікуванням і одиничною дисперсією кожна.

Знайти густину розподілу наступної комбінації цих величин:  Y=. Оформити результат графічно.

Задача 26

Система незалежних випадкових величин (,,,)має нормальну густину з нульовим математичним очікуванням і одиничною дисперсією кожна.

Знайти густину розподілу наступної комбінації цих величин:   Y=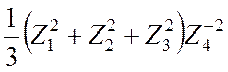. Оформити результат графічно.

Задача 27

Випадкова величина X має густину розподілу ймовірностей  ,  ; незалежна від неї випадкова величина Y має такий же закон розподілу.

Знайти густину розподілу різності Z=X–Y. Оформити результат графічно.

Задача 28

Випадкова величина X має густину розподілу ймовірностей   при   та   в протилежному випадку.  Випадкова величина Y має густину розподілу ймовірностей    при   та   в протилежному випадку.

Знайти розподіл ймовірностей випадкової величини Z = XY. Оформити результат графічно.

Задача 29

Система незалежних випадкових величин (,,,) має нормальну густину з нульовим математичним очікуванням і одиничною дисперсією кожна.

Знайти густину розподілу наступної комбінації цих величин:  Y=. Оформити результат графічно.

Задача 30

На інтервалі [0;a] випадкова обрана точка A. Після цього на том же інтервалі випадково обрана точка B.

Знайти ймовірність події {A:  точка В з’явилася зправа від точки А}.