Завдання по дисципліні “Теорія ймовірностей і математична статистика” для студентів механіко-математичного факультету. Модуль 2, страница 3

Елементи ()матриці являються незалежними випадковими величинами. Кожний з матричних елементів має математичне очікування, що дорівнює нулю, и дисперсію, що дорівнює .

Знайти математичне очікування та дисперсію визначника цієї матриці.

Задача  7

Знайти ексцес експоненціального розподілу, прийнявши його параметр таким, що заданий. Оформити результат графічно.

Задача 8

Випадкові величини X, X, …, X незалежні. Кожна з них приймає три значення: –1, 0, 1.  Відомо, що

Pr{X=1}=Pr{X=-1}=1/4,  Pr{X=0}=1/2,  (=1, 2, …, N).

Знайти математичне очікування ти дисперсію величини Z = .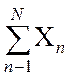

Задача 9

Випадкова величина X рівномірно розподілена на [0;1].

Потрібно знайти коефіцієнт кореляції двох випадкових величин Y=  та  Z=.

Задача 10

Випадкова величина X рівномірно розподілена на [0;1]. Випадкова величина Y приймає два значення: 0 и 1,  при цьому Pr(Y=0)=0,5  та  Pr(Y=1)=0,5.

Знайти закон розподілу випадкової величини Z=X+Y. Оформити результат графічно.

Задача 11

В області {(x+y)1} система випадкових величин (X,Y) має густину сумісного розподілу .

Знайти: коефіцієнт , густину розподілу ймовірностей  випадкової величини Z=(X+Y). Оформити результат графічно.

Задача 12

Випадкові величини X та Y незалежні та мають нормальний розподіл з параметрами (0,).

Знайти функцію розподілу випадкової величини Z=X+Y. Оформити результат графічно.

Задача 13

Випадкова величина Z має нормальний розподіл N(0; 1).

Знайти  M[cos(Z)]  и  D[cos(Z)].

Задача 14

Випадкова величина Z має нормальний розподіл N(0; 1).

Знайти M[cos(Z)]  и  M[sin(Z)].

Задача 15

В досліді одночасно кидають N шостиграних гральних кісток.

Знайти математичне очікування та дисперсію суми чисел очок, що випалі. Оформити результат графічно.

Задача 16

Площину розграфлено паралельними лініями, що розташовані друг от друга на відстані h. На площину наугад кинутий круг діаметром D, причому D<h.

Знайти ймовірність події:

{A: круг перетне яку-небудь пряму};

{B: круг не перетне ні одної з прямих}.

Оформити результат графічно.

Задача 17

Випадкові величини X і Y незалежні та нормально розподілені з нульовим математичним очікуванням і одиничною дисперсією.

З’ясувати, чи є незалежними дві випадковими величини U=X+Y  та  V=X–Y.

Задача 18

На інтервалі [0;a] випадково обрано точку A. Після чого на том же інтервалі випадково обрано точку B.

Знайти густину розподілу випадкової величини X, що дорівнює модулю довжини відрізка AB.

Задача 19

Густина розподілу випадкової величини X задана формулою  ,  якщо , та нулю в протилежному випадку.

Знайти: сталу A, функцію розподілу . Визначити значення ймовірностей Pr{>0.5} та Pr{0,25<X<0.5}.

Задача 20

Випадкова величина X визначена в інтервалі [0;2] і має густину розподілу ймовірностей .

Знайти столу A і обчислити Pr{<0.3}.

Задача  21

На площині задано два круга радіусом R кожний. Центр першого круга знаходиться в точці (R,R). Центр другого круга знаходиться в початку координат.

Знайти ймовірність того, що точка, яка 10 раз наугад кинута в перший круг, влучить 2 разу з них також і в другий.

Задача 22

Відомо, що два кореня рівняння x+px+q=0 мають випадкові значення з сталою густиною розподілу в інтервалі [–1;1] кожний.

Визначити густину розподілу ймовірностей  та  випадкових коефіцієнтів p і q.

Задача 23

Випадкові величини X і Y мають густину розподілу ймовірностей  ,  , та ,  .

Знайти закон розподілу випадкової величини Z=X+Y. Оформити результат графічно.

Задача 24

В області  випадкова величина X має густину розподілу ймовірностей  .

Знайти: сталу A, математичне очікування та дисперсію випадкової величини X.

Задача  25

В партії з 5 деталей є 3 дефектних. Наугад вибрано 3 деталі.

Побудувати ряд розподілу випадкової величини X – числа стандартних деталей серед вибраних, знайти M[X] і D[X].

Задача  26

Випадкові величини X і Y незалежні і нормально розподілені з нульовим математичним очікуванням і одиничною дисперсією.

З’ясувати, чи є незалежними дві випадкові величини U=2X+Y і V=X–2Y.

Задача  27

Випадкова величина X задана інтегральною функцією розподілу

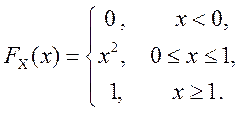
Знайти ймовірність того, що в результаті чотирьох незалежних іспитів величина X рівно три разу прийме значення в інтервалі [0,25; 0,75].

Задача 28

Діаметр круга вимірюван наближено.