Завдання по дисципліні “Теорія ймовірностей і математична статистика” для студентів механіко-математичного факультету. Модуль 2, страница 2

Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

12. Випадкова величина Х задана густиною розподілу ймовірностей:

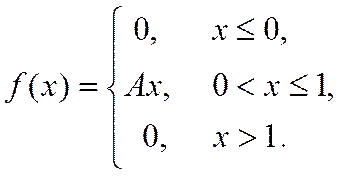
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

13. Випадкова величина Х задана густиною розподілу ймовірностей:

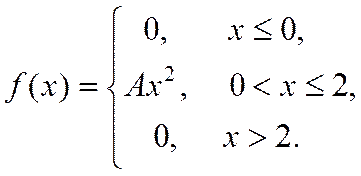
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

14. Випадкова величина Х задана густиною розподілу ймовірностей:

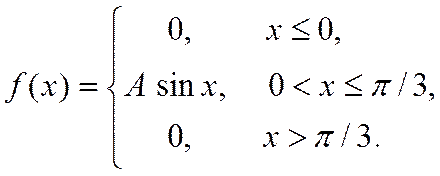
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

15. Випадкова величина Х задана густиною розподілу ймовірностей:

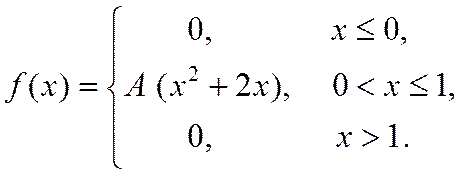
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

16. Випадкова величина Х задана густиною розподілу ймовірностей:

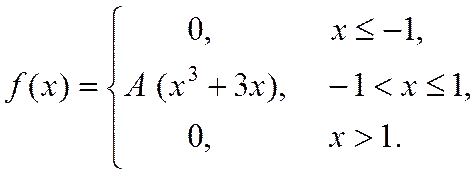
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

17. Випадкова величина Х задана густиною розподілу ймовірностей:

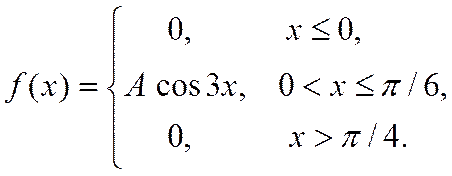
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

18. Випадкова величина Х задана густиною розподілу ймовірностей:

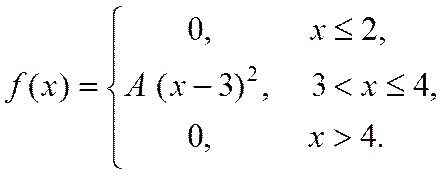
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

19. Випадкова величина Х задана густиною розподілу ймовірностей:

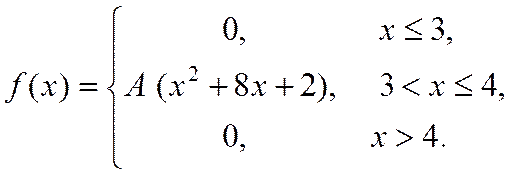
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

20. Випадкова величина Х задана густиною розподілу ймовірностей:

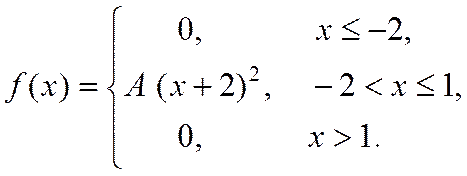
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

21. Випадкова величина Х задана густиною розподілу ймовірностей:

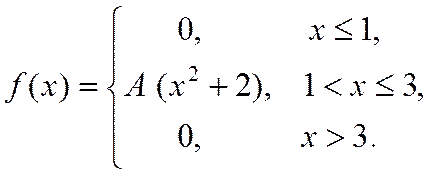
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

22. Випадкова величина Х задана густиною розподілу ймовірностей:

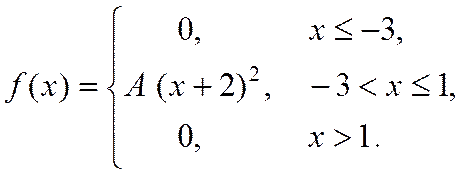
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

23. Випадкова величина Х задана густиною розподілу ймовірностей:

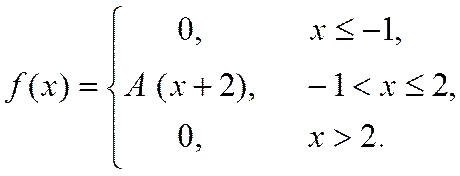
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

24. Випадкова величина Х задана густиною розподілу ймовірностей:

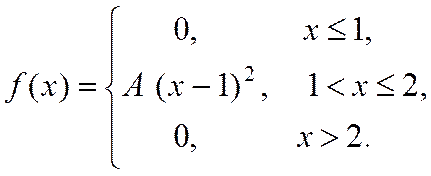
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

25. Випадкова величина Х задана густиною розподілу ймовірностей:

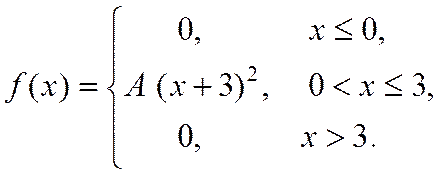
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

26. Випадкова величина Х задана густиною розподілу ймовірностей:

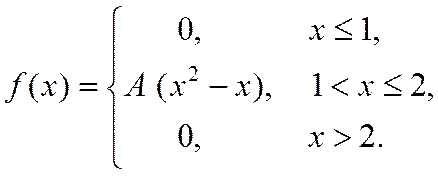
Знайти: параметр A;  функцію розподілу F(x);  математичне сподівання M[X];  дисперсію D[X];  ймовірність P(π/4≤X≤π). Роботу оформити графічно.

ЗАДАЧА  3   (ДЛЯ  ВСІХ  ВАРІАНТІВ)

Задача  1

Знайти густину розподілу випадкової величини, якій відповідає характеристична функція q(t)=sin(2t)/(2t). Оформити результат графічно.

Задача  2

Випадкова величина Z має показниковий розподіл з параметром . Знайти ймовірність P події . Оформити результат графічно.

Задача  3

Випадкова величина X має густину розподілу ймовірностей  ,  ; незалежна від неї випадкова величина Y має такий же закон розподілу.

Знайти густину розподілу випадкової різниці Z=X–Y. Оформити результат графічно.

Задача  4

Випадкова величина X рівномірно розподілена на [0;1].

Знайти  коефіцієнт  кореляції  випадкових  величин:  Y=(X–1/2) та  Z=(X–1/2).

Задача  5

Випадкова величина X рівномірно розподілена на [0;1].

Знайти коефіцієнт кореляції випадкових величин:  та .

Задача 6