Завдання по дисципліні “Теорія ймовірностей і математична статистика” для студентів механіко-математичного факультету. Модуль 2, страница 5

Випадкова величина X рівномірно розподілена на інтервалі [-1,1]. Відомо, що  Y=X.

Приймаючи, що цілочислений параметр m>0 є заданим, знайти коефіцієнт кореляції між випадковими величинами X і Y.

Задача 20

Дана випадкова величина X з густиною розподілу .

Знайти густину розподілу випадкової величини Y=tg(X). Оформити результат графічно.

Задача 21

Знайти закон розподілу випадкової величині, якому відповідає характеристична функція q(t)=cos(t). Оформити результат графічно.

Задача 22

Дана випадкова величина X з густиною розподілу .

Знайти густину розподілу випадкової величини Y=1/(1+X). Оформити результат графічно.

Задача 23

Випадкові величини X, X, X, X незалежні, позитивні та однаково розподілені.

Довести, що

M.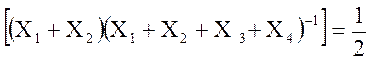

Задача 24

Знайти закон розподілу випадкової величини, якому відповідає характеристична функція q(t)=cos(t). Оформити результат графічно.

Задача 25

Знайти закон розподілу випадкової величини, якому відповідає характеристична функція q(t)=sin(t)/t. Оформити результат графічно.

Задача 26

Знайти закон розподілу випадкової величини, якому відповідає характеристична функція q(t)=(1–p)/[1–pexp(it)] з параметром p. Оформити результат графічно.

Задача 27

Випадкові величини X і Y незалежні та мають густини розподілу ймовірностей:

,  ,         .

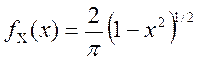Знайти закон розподілу випадкової величини Z=XY. Оформити результат графічно.

Задача 28

Знайти закон розподілу випадкової величини, якому відповідає характеристична функція q(t)=(3+cos(t))/4. Оформити результат графічно.

Задача 29

Відрізок довжиною d розламується в наугад обраної точці.  Знайти функцію розподілу випадкової величини – площі прямокутника, сторони якого дорівнюють частинам відрізка, що отримали. Оформити результат графічно.

Задача 30

Випадкова величина Z нормальна з нульовим математичним очікуванням та задано дисперсією .

Знайти закон розподілу випадкової величини U=|Z|. Оформити результат графічно.

ЗАДАЧА  5  (ДЛЯ  ВСІХ  ВАРІАНТІВ)

Задача  1

Кусок тонкої проволоки довжиною 20см зігнули в наугад обраної точці (точка згинання рівномірно розподілена по куску). Після цього, перегнувши проволоку ще в двох місцях (не зламуючи), зробили прямокутну рамку.

Знайти ймовірність того, що площина рамки не перевищує 21см.

Задача  2

Знайти густину розподілу ймовірностей суми Z=X+Y двох визначених на всієї числової вісі незалежних випадкових величин X и Y, що підпорядковуються законам

,   ,      .

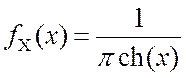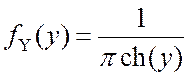Оформити результат графічно.

Задача  3

Випадкова величина X розподілена за законом  з k степенями вільності.  Випадкова величина Y розподілена за законом  з j степенями вільності.

Знайти закон розподілу випадкової величини Z=X+Y. Оформити результат графічно.

Задача 4

Випадкова величина X має неперервну функцію розподілу ймовірностей .

Знайти густину розподілу  ймовірностей випадкової величини Y=. Оформити результат графічно.

Задача  5

Випадкові величини , ,  незалежні та нормально розподілені з математичним очікуванням m=0 і дисперсією D=1 кожна.

Знайти густину розподілу ймовірностей  випадкової величини  Y=. Оформити результат графічно.

Задача 6

На колі радіусом R випадково обирається точка A. Закон розподілу її азимута – рівномірний. Після цього незалежно обирається точка B. Закон розподілу її азимута також рівномірний.

Знайти закон розподілу випадкової довжини хорди AB. Оформити результат графічно.

Задача 7

Знайти коефіцієнт , характеристичну функцію випадкової величини X, яка має густину розподілу ймовірностей

,   ,

з заданими m – цілим та b – позитивним параметрами. Оформити результат графічно.

Задача 8

Випадкова величина X підпорядковується розподілу Пуассона з параметром . Незалежна від неї випадкова величин Y підпорядковується такому ж розподілу.

Знайти закон розподілу випадкової величини Z=X–Y. Оформити результат графічно.

Задача 9

Над площиною x0y на висоті h підвішений точкове джерело світла, випромінювання якого рівномірно направлено в усі сторони. На площині розміщений фотопапір, що реєструє випромінювання.

Знайти закон розподілу степені засвітлення фотопаперу. Оформити результат графічно.

Задача 10

Випадкова величина X рівномірно розподілена на інтервалі , а випадкова величина Y рівномірно розподілена на інтервалі .

Знайти закон розподілу випадкової величини Z=X+Y. Оформити результат графічно.