Математика \ Теория вероятности

Завдання по дисципліні “Теорія ймовірностей і математична статистика” для студентів механіко-математичного факультету. Модуль 2, страница 4

Приймаючи, що його величина рівномірно розподілена на відрізку [a,b], знайти закон розподілу ймовірностей випадкової площі круга. Оформити результат графічно.

.

Задача 29

Випадкова величина X має густину розподілу ймовірностей  при  та  при . Розглядається випадкова величина Y=X[1–exp(-X)],  де >0.

Знайти математичне очікування і дисперсію випадкової величини Y.

Задача  30

В кругу  густина розподілу ймовірностей  випадкових величин X і Y наступна: ,  поза круга вона дорівнює нулю.

Знайти: a) сталу A;  б) ймовірність влучення випадкової точки (X,Y) в круг радіусом  r=2 з центром в початку координат, якщо R=4. Оформити результат графічно.

ЗАДАЧА 4   (ДЛЯ  ВСІХ  ВАРІАНТІВ)

Задача  1

Густина розподілу ймовірностей  двовимірної системи випадкових величин (X,Y) стала в одиничному квадраті (01) і дорівнює 1.

Визначити, чи є випадкові величини X і Y незалежними.

Задача  2

Центр круга радіусом R знаходиться у точці (0,0). Центр квадрату зі стороною 2h співпадає з точкою (0,0), а сторони його паралельні координатним осям.

Знайти ймовірність того, що точка, що наугад кинута в круг, влучить також і в квадрат.

Задача  3

Випадкові величини X і Y незалежні і розподілені рівномірно:  X в інтервалі [a,b],  Y – в інтервалі [c,d].

Знайти дисперсію випадкової величини Z=XY.

Задача  4

Випадкові величини X, X, X, X, X, X незалежні, позитивні та однаково розподілені.

Довести, що

M.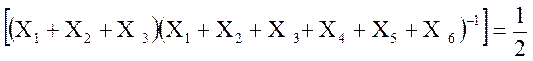

Задача  5

Заданий інтегральний розподіл ймовірностей  випадкової величини X.  Випадкова  величина Y  пов’язана з величиною X співвідношенням Y=6X–6.

Знайти інтегральний розподіл ймовірностей  випадкової величини Y. Оформить результат графічно.

Задача  6

Знайти характеристичну функцію дискретної випадкової величини X, що підпорядковувається закону

Pr{X=a} = ,   a>0,  m = 0, 1, 2, …,

і за неї визначити M[X] і D[X].

Задача  7

Випадкова величина Z нормальна з нульовим математичним очікуванням і заданої дисперсії .

Знайти значення дисперсії, за якою ймовірність Pr{pZq} буде найбільшою (параметри p і q задані та позитивні, pq).

Задача  8

Серед 25 білетів 5 "добрих". Два студента по черзі беруть по одному білету. Знайти ймовірність того, що:

a) перший студент узяв "добрий" білет;

б) другий студент узяв "добрий" білет;

в) обидва студенти взяли "добрі" білети.

Задача  9

Випадкова величина X рівномірно розподілена на [–1;1].

Приймаючи параметри p и q такими, що задано, знайти коефіцієнт кореляції випадкових величин Y=pX  і  Z=qX.

Задача 10

Система нормальних випадкових величин (X,Y) має такі параметри: математичні очікування  і ; середньоквадратичні відхили  і ;  коефіцієнт кореляції r.

Знайти лінійне перетворення випадкових величин (X,Y) до незалежних випадковим величинам (U,V) і визначити дисперсії нових випадкових величин. Оформити результат графічно.

Задача 11

Задано інтегральний розподіл ймовірностей  випадкової величини X. Випадкова величина Y пов’язана з величиною X співвідношенням Y=2+X/3.

Знайти інтегральний розподіл ймовірностей  випадкової величини Y. Оформити результат графічно.

Задача 12

Випадкова величина X рівномірно розподілена на [0;1].

Приймаючи, що параметри p і q задано, знайти коефіцієнт кореляції випадкових величин  Y=pX  і  Z=qX.

Задача 13

Сумісна густина розподілу ймовірностей випадкових величин (X,Y) наступна

,       .

Знайти закон розподілу випадкової величини  U=X+Y. Оформити результат графічно.

Задача 14

Координати випадкової точки (X,Y) на площині утворюють систему з густиною розподілу ймовірностей

,     .

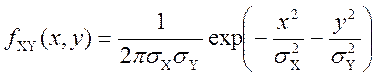Знайти густину розподілу ймовірностей  випадкової фази  =arctg(Y/X)  точки з координатами (X,Y). Оформити результат графічно.

Задача 15

Дана випадкова величина X з густиною розподілу .

Знайти густину розподілу випадкової величини Y=(R–X). Оформити результат графічно.

Задача 16

Дана випадкова величина X з густиною розподілу .

Знайти густину розподілу випадкової величини Y=arctg(X). Оформити результат графічно.

Задача 17

Випадкова величина X розподілена за законом Пуассона з параметром .  Відомо, що Y=X.

Найти M[Y], D[Y].

Задача 18

Дана випадкова величина X з густиною розподілу  .

Знайти густину розподілу випадкової величини Y=exp(-X). Оформити результат графічно.

Задача 19

Скачать файл