Задача 1
Перевірялась робота аварійного відключення електромеханічної системи. Для цього були створені екстремальні умови і фіксувались моменти t аварійного відключення.(див таблицю)

1. Побудувати інтервальний варіаційний ряд.
2. Підрахувати вибіркові
характеристики: середнє![]() , дисперсію
, дисперсію ![]() і середнє квадратичне відхилення
і середнє квадратичне відхилення ![]() , медіану
, медіану ![]() і моду
і моду ![]() .
.
3. Побудувати полігон і гістограму.
4. Знайти емпіричну функцію розподілу.
Розв’язання
Запишемо статистичні дані в неспадному порядку:
0,256; 0,471; 0,614; 0,682; 0,738; 0,774; 0,917; 0,917; 0,919; 1,008; 1,043; 1,069; 1,124; 1,125; 1,586; 1,733; 1,75; 1,895; 1,956; 2,03; 2,032; 2,083; 2,13; 2,472; 2,514; 2,563; 2,57; 2,921; 3,093; 3,096; 3,3; 3,418; 3,483; 3,736; 3,854; 3,924; 4,116; 4,437; 4,536; 4,614; 5,124; 5,795; 6,679; 7,259; 7,599; 11,12; 12,57; 14,89; 15,33;
Знаходимо розгін варіації: R=tmax-tmin=15,074;
Визначаємо оптимальний інтервал, довжину інтервалу h:
h=R/k;
k=1,73*n^1/3=6,373374493;
h =2,36515209;
Обчислюємо межі:
α1=tmin-h/2=-0,994![]() -1;
-1;
α2=α1+h=1,506![]() 1,5;
1,5;
Отримуємо інтервальний варіаційний ряд:
|
|
(-1;1.5] |
(1,5;4] |
(4;6,5] |
(6.5;9] |
(9;11,5] |
(11,5;14] |
(14;16,5] |
|
|
14 |
23 |
6 |
3 |
1 |
1 |
2 |
|
|
0,28 |
0,46 |
0,12 |
0,06 |
0,02 |
0,02 |
0,04 |
|
|
0,25 |
2,75 |
5,25 |
7,75 |
9,25 |
11,75 |
13,25 |
Підраховуємо вибіркові характеристики:
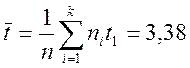
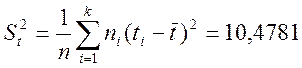
![]()
![]()
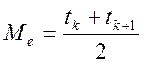 , так як
, так як ![]()
![]()
![]() - це елемент вибірки, який зустрічається
найчастіше.
- це елемент вибірки, який зустрічається
найчастіше.
![]()
Будуємо полігон:
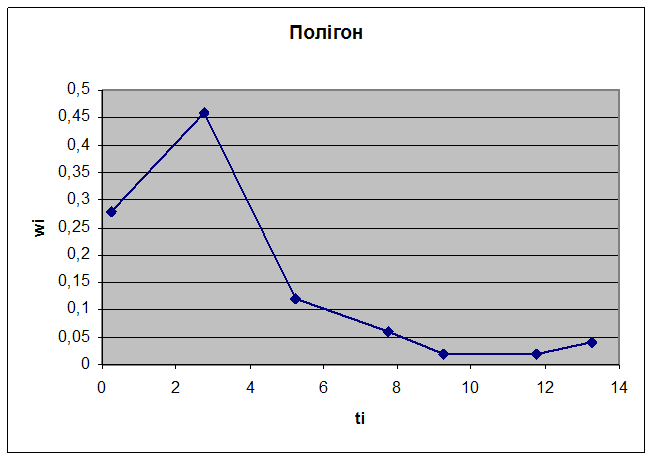
Гістограма буде мати вигляд:
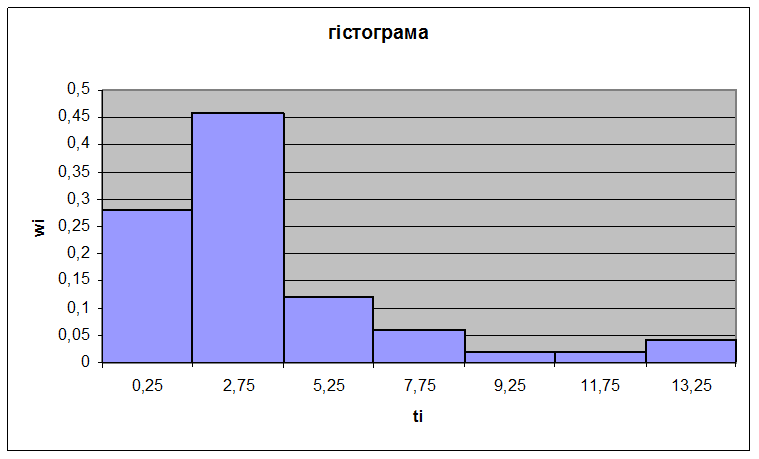
Тепер запишемо аналітичний вигляд емпіричної функції розподілу:
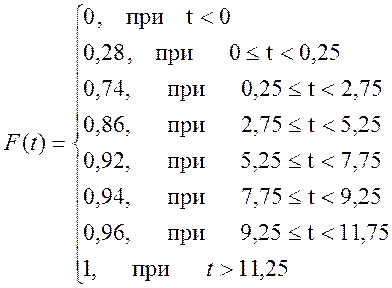
Задача 3
Випадкова величина Х (маса тіла дорослої людини)
розподілена за нормальним законом з параметрами mта ![]() . У результаті статистичних
досліджень, отримано такий статистичний розподіл маси дорослих людей для n=1000 осіб.
. У результаті статистичних
досліджень, отримано такий статистичний розподіл маси дорослих людей для n=1000 осіб.
|
Маса тіла, кг |
(45;55) |
(55;65) |
(65;75) |
(75;85) |
(85;95) |
(95;105) |
(105;115) |
(115;125) |
|
Кількість осіб |
57-k |
136+p |
223+s |
249-n-s |
191-p |
100+n |
36+k-m |
8+m |
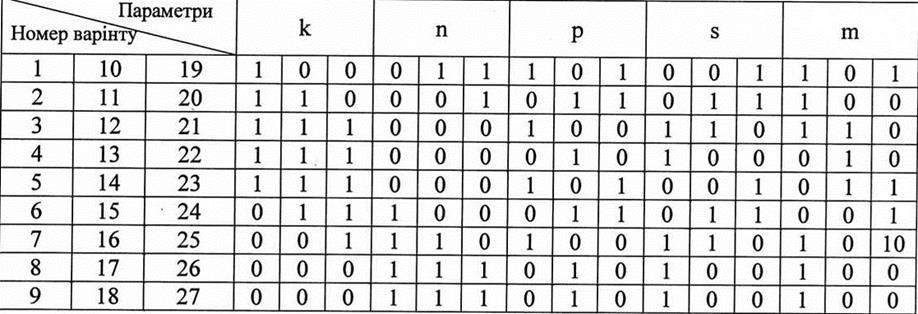 Знайти методом моментів точкову
оцінку невідомих параметрів mта
Знайти методом моментів точкову
оцінку невідомих параметрів mта ![]() . Дані параметрів для невідомих параметрів наведені в таблиці
. Дані параметрів для невідомих параметрів наведені в таблиці
Розв’язання
З врахуванням невідомих параметрів отримуємо:
|
Маса тіла, кг |
(45;55) |
(55;65) |
(65;75) |
(75;85) |
(85;95) |
(95;105) |
(105;115) |
(115;125) |
|
Кількість осіб |
57 |
137 |
224 |
247 |
190 |
101 |
35 |
9 |
Переходимо до точкового ряду:
|
Маса тіла, кг |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
|
Кількість осіб |
57 |
137 |
224 |
247 |
190 |
101 |
35 |
9 |
Оскільки нормальний розподіл визначається двома параметрами, то точкові оцінки визначаємо за формулами:
![]()
![]()
Тепер обрахуємо вибіркову дисперсію та середнє вибіркове:
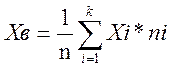
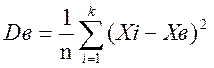
Підставивши дані отримаємо: ![]()
![]() ,
, ![]()
Отже точкові оцінки параметрів mта ![]() дорівнюють:
дорівнюють:
m *=78,64
![]() *=231,9504
*=231,9504
Відповідь: m *=78,64 та ![]() *=231,9504
*=231,9504
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.