Розв’язання задач на пошук сталої, математичного сподівання, ймовірності та їх відношення

Сумський Державний Університет

Кафедра моделювання складних систем

Завдання

з дисципліни

“Теорія ймовірностей і математична статистика”

(п’ятий семестр)

МОДУЛЬ 3

Варіант 8

Виконав: студент групи  ІН-83

Кримець П. В.

Перевірив: проф. Мазманішвілі О.С.

Суми – 2011

Задача 1

Густина розподілу  випадкової величини X має вигляд

,       .

В задачі потрібно:

1. Знайти сталу .

2. Знайти математичне сподівання .

3. Розглянувши випадкові події  та , знайти ймовірності ,  та їх відношення .

4. Оформити результати графічно.

Параметри:

k = 3,      m = 1,      n = 2,      p = 1.

Розв’язання

Підставимо задані параметри і отримаємо густину розподілу  випадкової величини X, яка має вигляд:

,

1.  Знайти сталу .

Густина f(x) будь-якої випадкової величини невід'ємна, f(x) > 0, та має властивість

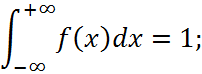
тобто ймовірність повної групи подій дорівнює одиниці.

Коефіцієнт С визначимо за допомогою формули про ймовірність повної групи подій:

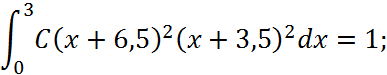
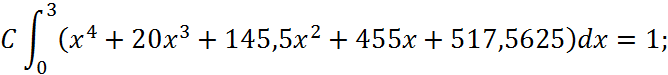
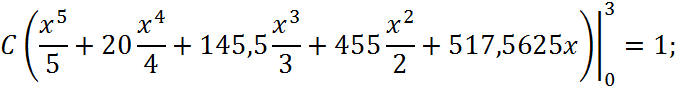
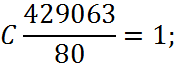
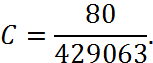
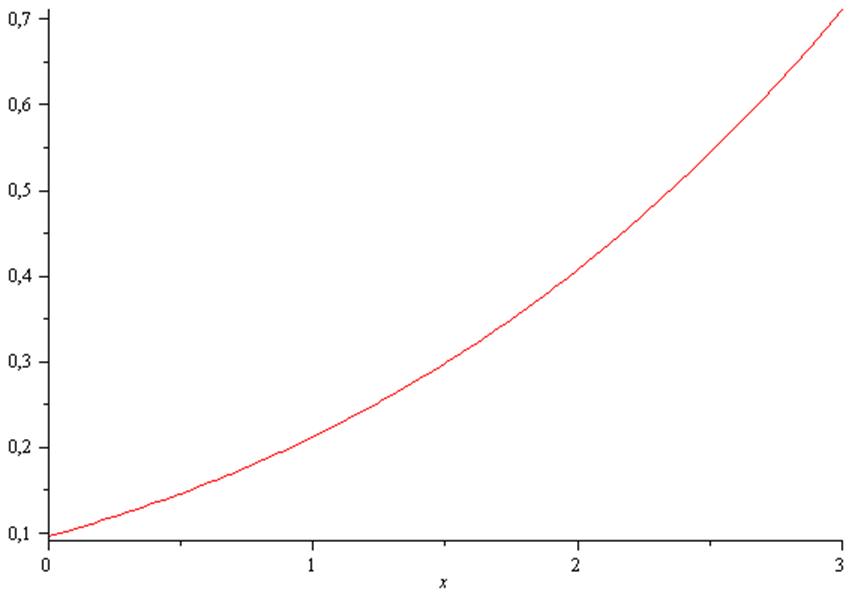
Рис. 1 - Графік густини

2.  Знайти математичне сподівання .

Математичним сподіванням неперервної випадкової величини X з густиною f(x) називається її середнє значення, що обчислюється за формулою

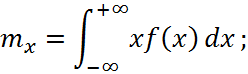
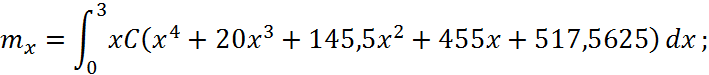
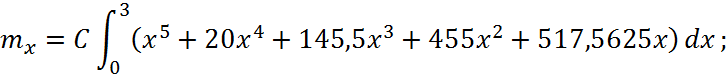
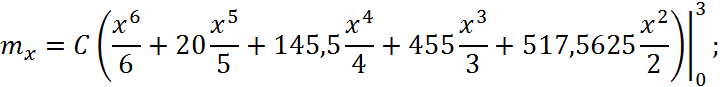
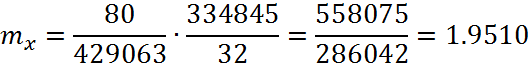
3.  Розглянемо подію . Оскільки, за умовою  то розіб’ємо інтервал на дві частини по . Отримаємо, що  і

 . Тоді у термінах інтегральної функції розподілу буде обчислюватися як:

І аналогічно обчислюється :

Спочатку знайдемо

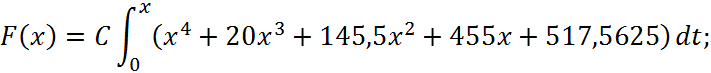
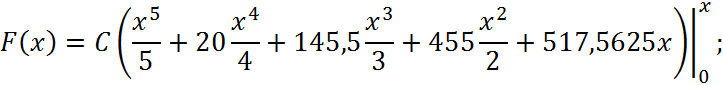
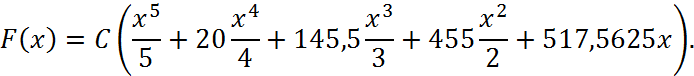
Обчислимо ймовірність :

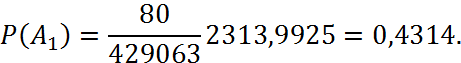
Тепер знайдемо ймовірність :

Отже,

Задача 2

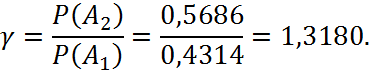
Результати дослідження міцності на стиснення (випадкова величина X) 200 зразків бетону представлені в вигляді статистичного ряду:

Інтервали міцності,  кг/см	Частоти,
190–200	10
200–210	26
210–220	56
220–230	64
230–240	30
240–250	14

Потрібно перевірити нульову гіпотезу про нормальний закон розподілу міцності на стиснення. Рівень значущості прийняти =0,10 та  = 0,05. Результати оформити графічно.

Розв’язання

З умови слідує, що точні параметри гіпотетичного нормального закону нам не відомі, тому нульову гіпотезу можна сформулювати наступним чином:

{H₀: F(x) є функцією нормального розподілу } з параметрами  і

Для перевірки цієї нульової гіпотези визначимо значення x_i^*середин інтервалів і знайдемо точкові оцінки математичного очікування і середньо-квадратичного відхилення нормально розподіленої випадкової величини за формулами:

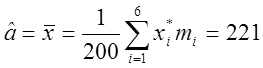 кг/см²;

;

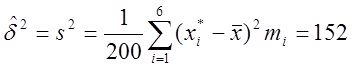 кг/см².

          Обчислимо теоретичну ймовірність pⁱпотрапляння випадкової величини в частинні інтервали [x_i-1;x_i] за формулою:

           

 

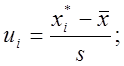
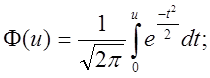
Подальші обчислення необхідні для визначення спостережуваного значення вибіркової статистики Х² зведено в таблиці, де Q_i=(m_i-np­_i)² і R_i=(m_i-np­_i)²/np­_i

i	Інтервал	mi	pi	npi	Qi	Ri
1	190-200	10	0,0443	8,8507	1,3208	0,1492
2	200-210	26	0,1419	28,3769	5,6496	0,1991
3	210-220	56	0,2815	56,3078	0,0947	0,0017
4	220-230	64	0,2996	59,9254	16,6026	0,2771
5	230-240	30	0,1711	34,2101	17,7248	0,5181
6	240-250	14	0,0617	12,3292	2,7917	0,2264
Суми:		200	1.0000	200,00	44,1842	1,3716

В результаті обчислень знаходимо: Х²_набл=1,37

За таблицею квантилей Х² розподілу за заданими рівням значущості α=0,05, α=0,1 та числу степенів свободи 3 знайдемо значення Х²_0,05;3=7.82, Х²_0,1;3=9.41

Так як 1,37 < 7.82, а також 1,37 < 9,41 ми приймаємо нульову гіпотезу в обох випадках

Відповідь

Експериментальні данні розподілені за нормальним законом з α=221 та δ²=152

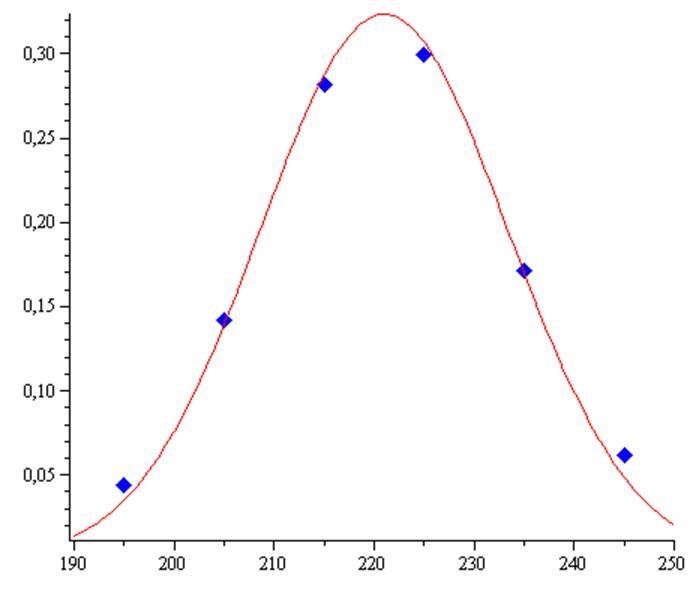
          Рис. 2 - Графік розподілу

Задача  3

Стверджується, що результат дії ліків залежить від способу їх застосування.

Перевірити це твердження при  = 0,10 та  = 0,05.

Результат	Спосіб 1	Спосіб 2	Спосіб 3
Несприятливий	11	17	16
Сприятливий	20	23	19

Розв’язання

За заданими даними побудуємо таблицю:

Результат	Спосіб 1	Спосіб 2	Спосіб 3	Всього (vi)
Несприятливий	11	17	16	44
Сприятливий	20	23	19	62
Всього (uj)	31	40	35	212

Перевіримо гіпотезу H₀  про незалежність двох ознак: дії ліків X і способу їх застосування Y. Для цього за критерієм χ² використовуємо статистику:

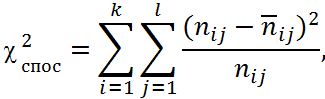
де n_ij - число виходів,   в яких реалізовувалася подія;

  - очікувані частоти,   - очікувані частості.

В рамках гіпотези про незалежність ознак X та Y маємо   де р_i - ймовірності влучення X в i-й інтервал (і = 1,..., к),  р_j - ймовірності влучення Y в

j-й. інтервал (j = 1,...,l), відповідно. Тоді маємо: