13 Знайти ймовірність того, що в n незалежних випробуваннях подія А настане рівно М раз, якщо ймовірність настання А в кожному з них однакова і дорівнює р.
Додаткова інформація. а) n; M; p, б)n; M; p.
13.1 a)8; не менше 2 і менше 6; 0,01
б) 300;мене 71; 0,2
Розв’язок.
Нехай
А – подія, задана умовою а);
В – подія задана умовою б).
Тоді
а) ймовірність Р(А), враховуючи відносно невелике n, шукаємо використовуючи формулу Бернуллі, точніше одну з її властивостей,
P(A)=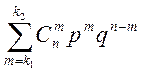
Маємо
P(A)=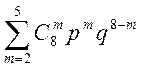 =
=
=![]()
![]() =
=
=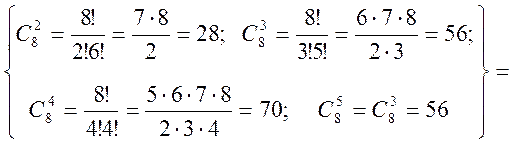
=![]()
+![]() =
=
=0,002690…
б) Ймовірність Р(В) шукаємо використовуючи інтегральну теорему Муавра-Лапласа
Pn(а,b)![]()
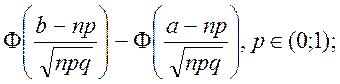
Маємо
P(B)=P300(0;70)![]()
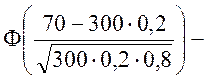
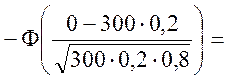
![]()
Відповідь: Р(А)=0,002600...; Р(В)=0,9251
13.2 а) 300; 2 або 3; 0,01
б) 300; більше 190 і не більше 193; 0,6.
Розв’язок.
Нехай
А – подія задана умовою а);
В – подія задана умовою б).
Тоді а), оскільки р=0,01 < 0,1 і npq=300·0,01·0,99=3·0,99 < 9
Ймовірність Р(А) шукаємо за формулою Пуасона
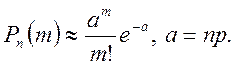
Маємо:
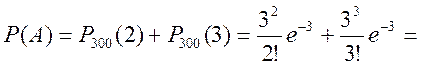

б) ймовірність Р(В), оскільки
р=0,6 > 0,5 і npq=300·0,6·0,4 = 72 > 10,
шукаємо за формулою Мавра - Лапласа
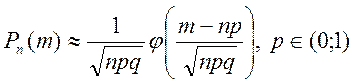
Маємо
![]()
![]()
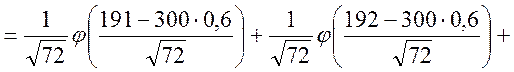
![]()
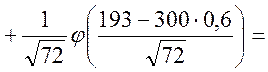
![]()
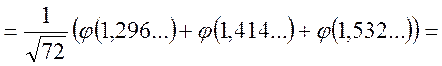
![]()
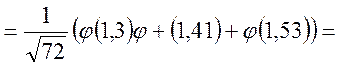
![]()
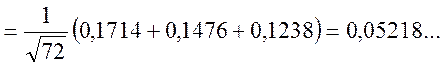
Відповідь: Р(А)=0,4480...; Р(В)=0,05218...
15 Дана
рівність, яка на заданому проміжку визначає функцію (щільність) розподілу
неперервної випадкової величини X. Потрібно: а) знайти параметр ![]() і щільність (функцію) розподілу, виписати
задану і знайдену функцію
і щільність (функцію) розподілу, виписати
задану і знайдену функцію ![]() і побудувати її
графіки; б) обчислити числові характеристики
і побудувати її
графіки; б) обчислити числові характеристики ![]() і
ймовірність
і
ймовірність ![]() .
.
Додаткова інформація: ![]() або
або ![]() та її
область ненульових значень;
та її
область ненульових значень; ![]() .
.
15.1 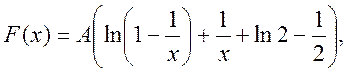
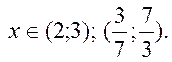
Розв’язок.
а) Параметр
А шукаємо з умови, що ![]() на правому кінці її область
ненульових значень дорівнює.
на правому кінці її область
ненульових значень дорівнює.
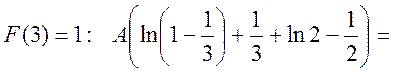
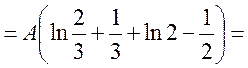
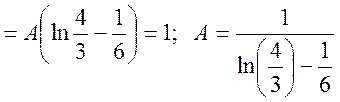 .
.
Отже
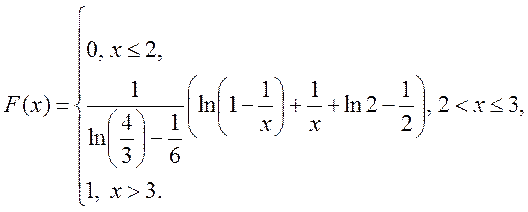 (А)
(А)
Знайдемо
щільність розподілу ![]() , використовуючи співвідношення
, використовуючи співвідношення ![]() .
.
Маємо
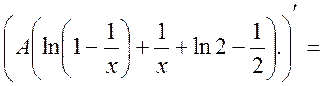
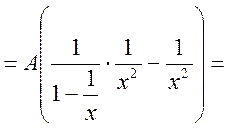
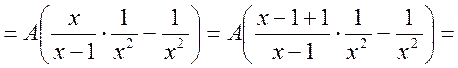
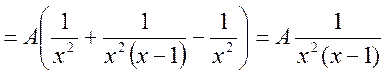
Отже
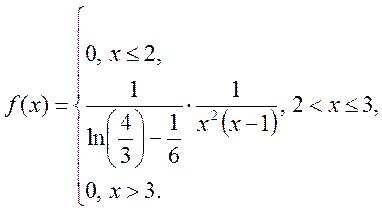 (В)
(В)
Графіки F(x) i f(x), приблизно мають вид
![]() y
y
y=F(x)
![]()
 1 ‑‑‑
1 ‑‑‑
![]()
![]() | | |
| | |
0 1 2 3 x
![]() (C)
(C)
y

![]() 2 ‑‑
2 ‑‑
y=f(x)
![]() 1 ‑‑
1 ‑‑
![]()
![]()
![]() | | |
| | |
0 1 2 3 x
б) Шукаємо числові характеристики випадкової величини X.
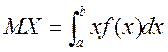
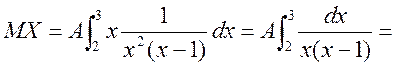
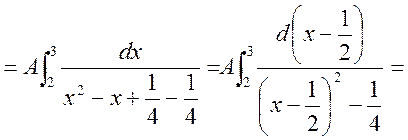
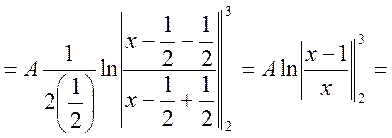
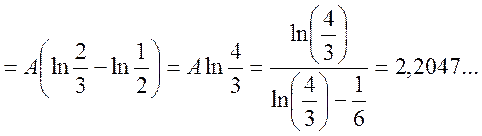 ;
;
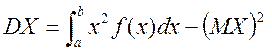
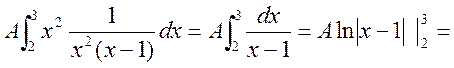
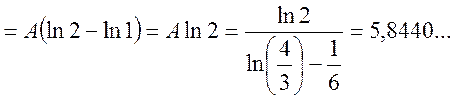
![]() ;
;
![]() ю
ю
Шукаємо
ймовірність ![]()
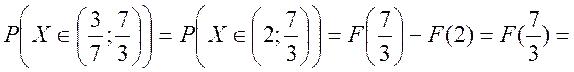
=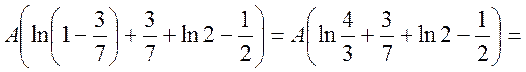
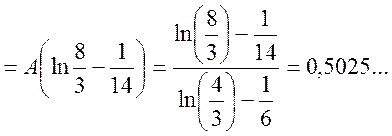 .
.
Відповідь: ![]() ;
;
![]()
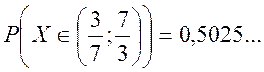 .
.
15.2 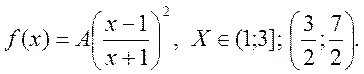
Розв’язок
а) Параметр А шукаємо з умови
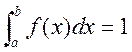
Маємо
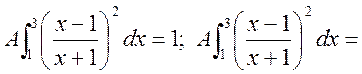
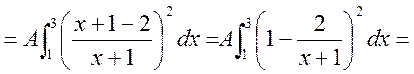
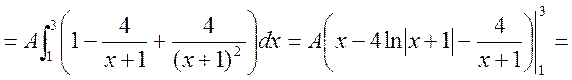
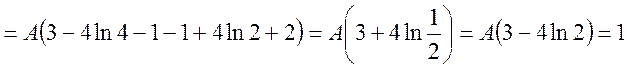 ,
,
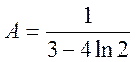 .
.
Отже
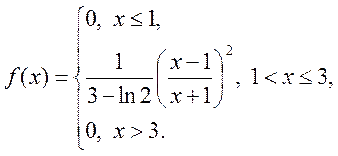 (А)
(А)
Знаходимо функцію розподілу F(x) використовуючи співвідношення
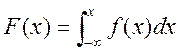
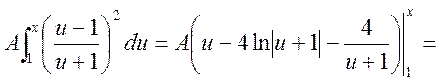
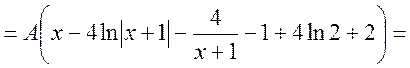
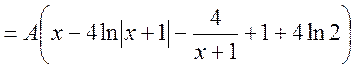 .
.
Отже
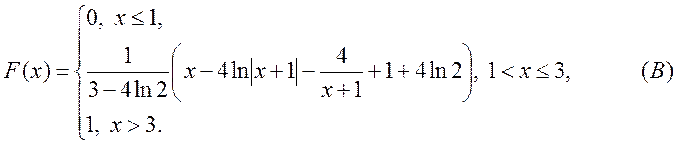 Графіки F(x)
i f(x), приблизно , мають вид
Графіки F(x)
i f(x), приблизно , мають вид
![]() y
y
y=F(x)
 |
|||
![]()
![]()
![]() | | |
| | |
0 1 2 3 x
![]() y
y
![]()

y=f(x)
![]()
![]()
![]() | | |
| | |
0 1 2 3 x
б) Шукаємо числові характеристики випадкової величини X.
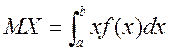
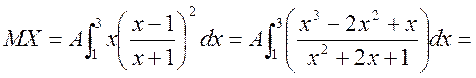
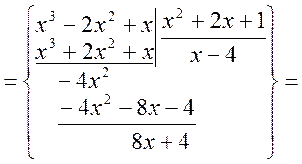
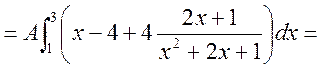
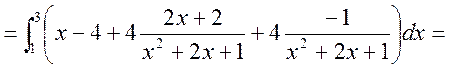
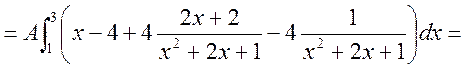
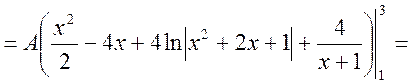
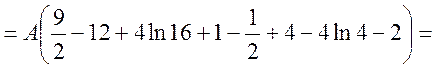
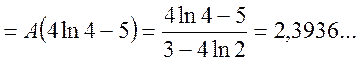 ;
;
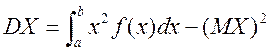
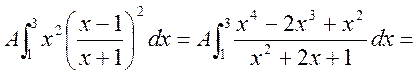
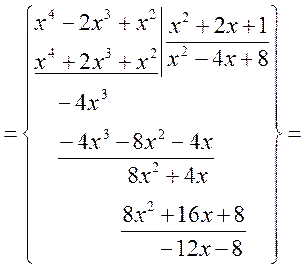
=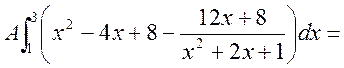
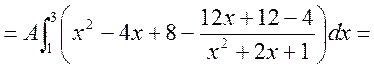
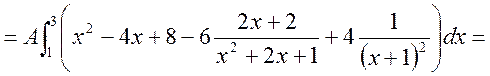
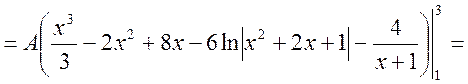
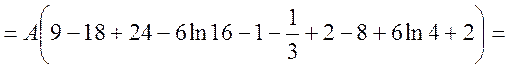
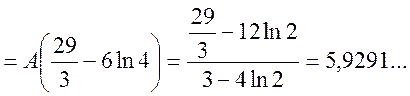
![]() ;
;
![]() .
.
Шукаємо
ймовірність ![]()
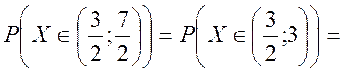
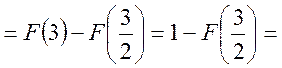
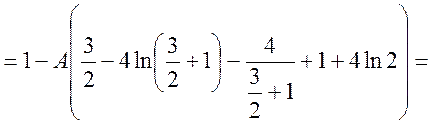
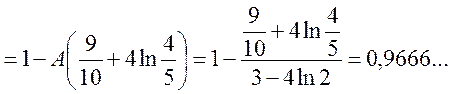 .
.
Відповідь: ![]()
![]()
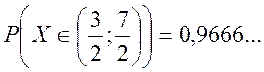 .
.
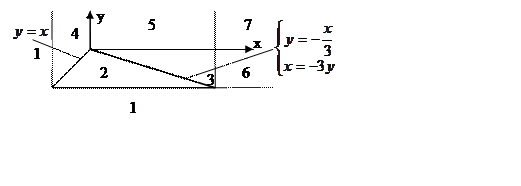
17 Двовимірна випадкова величина ![]() має
рівномірний розподіл в області
має
рівномірний розподіл в області ![]() . Потрібно: а) знайти
розподіли
. Потрібно: а) знайти
розподіли ![]()
![]() ; б) обчислити
; б) обчислити ![]()
![]() ,
, ![]() ; в) виписати коваріаційну матрицю,
вияснити
; в) виписати коваріаційну матрицю,
вияснити ![]() залежні (незалежні), корельовані (некорельовані).
залежні (незалежні), корельовані (некорельовані).
 |
Розв’язок
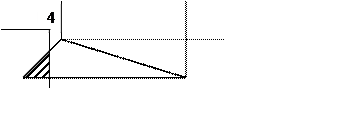
а) Шукаємо розподіли враховуючи, що випадкова величина ![]() рівномірно розподілена лише в області
рівномірно розподілена лише в області ![]() площини
площини ![]() , а не
на всій площині
, а не
на всій площині ![]() .
.
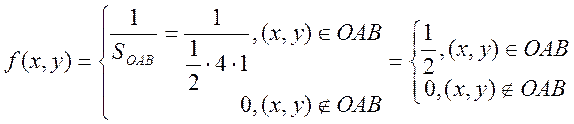 (А)
(А)
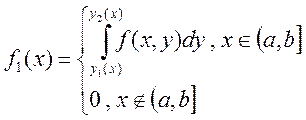 -
-
де інтеграл справа в ![]() є інтегралом від
параметра
є інтегралом від
параметра ![]() .
.
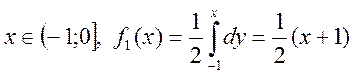
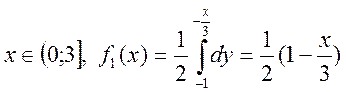
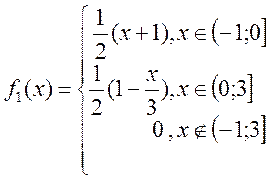
![]()
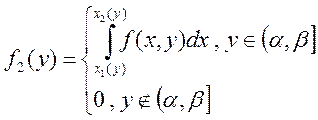 -
-
де інтеграл справа в ![]() є інтегралом від
параметра
є інтегралом від
параметра ![]() .
.
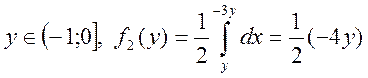
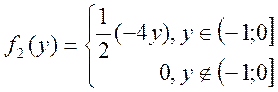
![]()
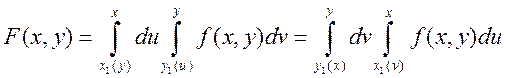 -
-
інтеграл із змінними верхніми межами інтегрування.
Тут
![]() - числа,
- числа, ![]() -
функції.
-
функції.
1. 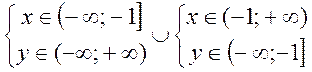
![]() , оскільки в цій області
, оскільки в цій області ![]() .
.
 2.
2. 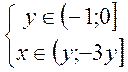
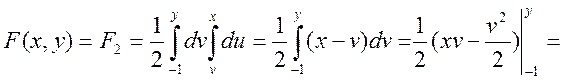
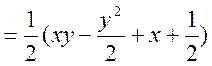
Звичайно ж
можна![]() для області 2 знайти і таким способом
для області 2 знайти і таким способом
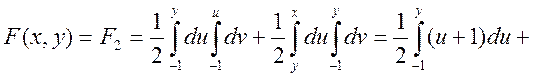
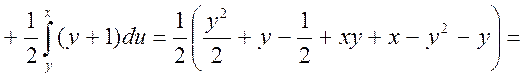

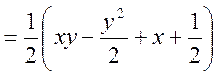
3. 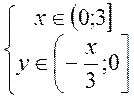
![]()
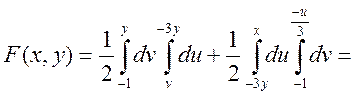
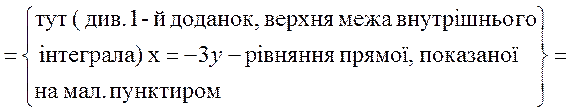
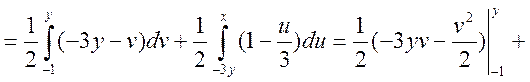
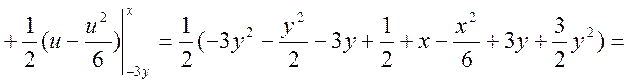
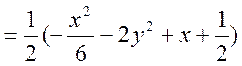
Або
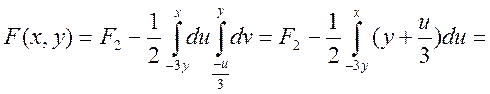
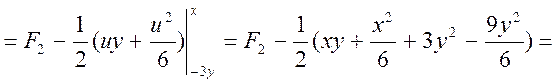
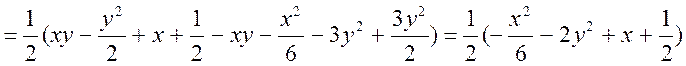
 |
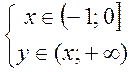
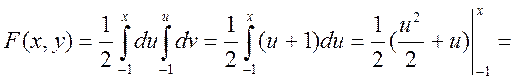

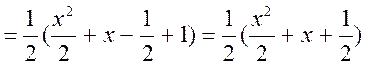
5. 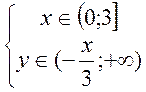
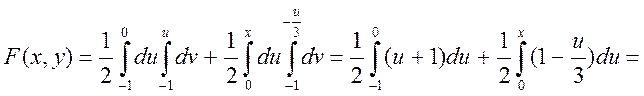
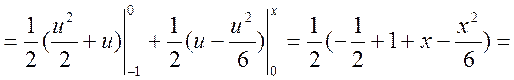
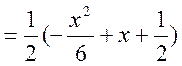
Або
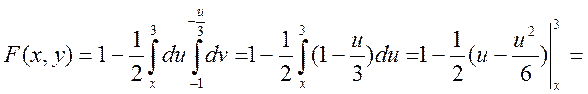
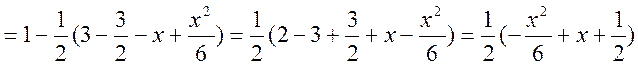
 6.
6. 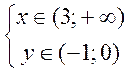
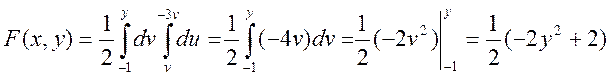
 |
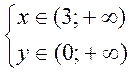
![]()
Таким чином
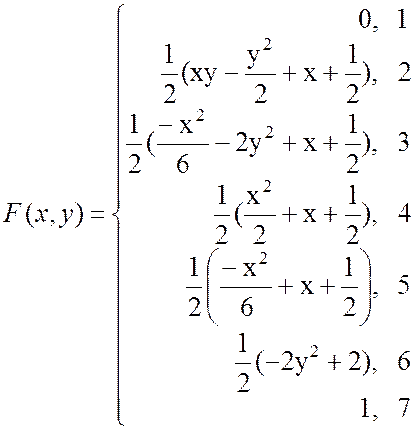
![]()
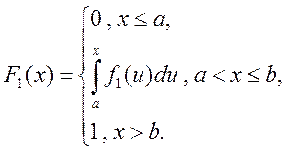
де 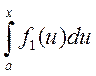 — інтеграл із змінною верхнею межею
інтегрування.
— інтеграл із змінною верхнею межею
інтегрування.
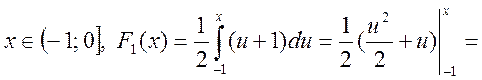
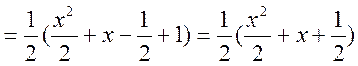
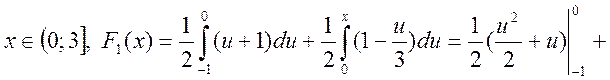
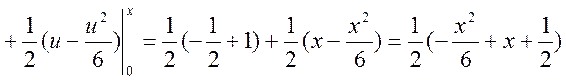
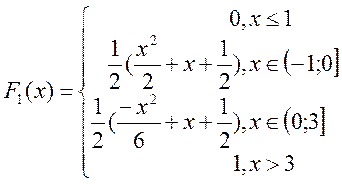
![]()
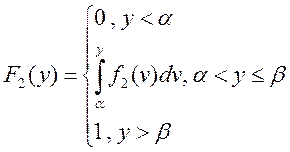 -
-
де 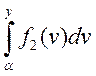 — інтеграл із змінною верхнею межею
інтегрування.
— інтеграл із змінною верхнею межею
інтегрування.
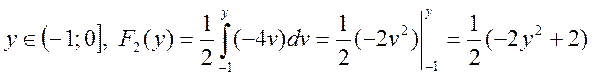
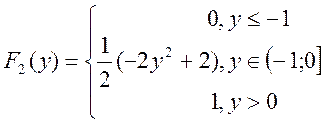
![]()
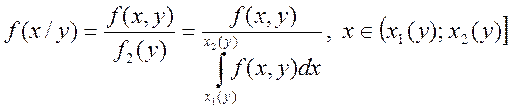
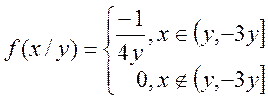
![]()
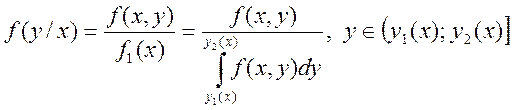
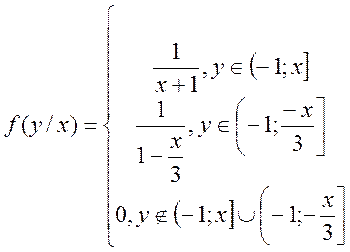
![]()
![]() — функція регресії
— функція регресії ![]() на
на
![]() (або умовне математичне сподівання
складової
(або умовне математичне сподівання
складової ![]() при заданому
при заданому ![]() ) є неперервною
випадковою величиною із щільністю розподілу
) є неперервною
випадковою величиною із щільністю розподілу ![]() .
Знаходиться
.
Знаходиться ![]() за формулою
за формулою
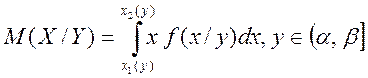 ,
,
де ![]() — функції
— функції ![]() .
.
Отже
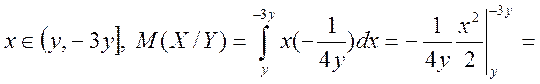
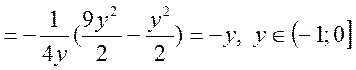
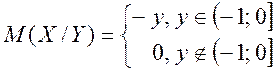
![]()
![]() — функція регресії
— функція регресії ![]() на
на
![]() (або умовне математичне сподівання
складової
(або умовне математичне сподівання
складової ![]() при заданому
при заданому ![]() ) є неперервною
випадковою величиною із щильністю розподілу
) є неперервною
випадковою величиною із щильністю розподілу ![]() .
Знаходять
.
Знаходять ![]() за формулою
за формулою
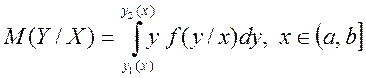 ,
,
де ![]() — функції
— функції ![]() .
.
Отже
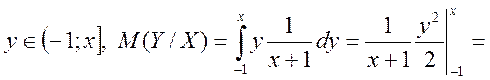
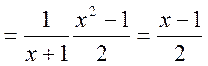
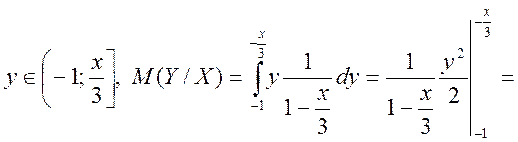

Таким чином
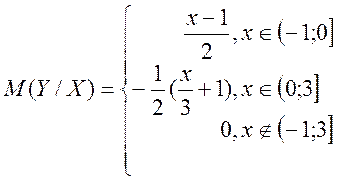
![]()
б) Обчислюємо числові характеристики
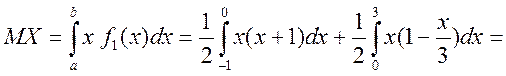
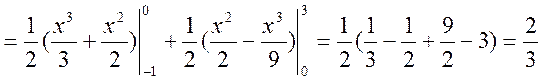
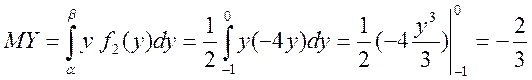
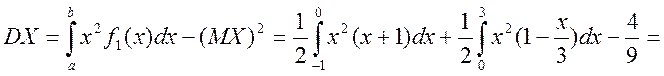
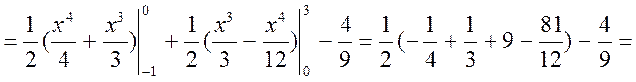
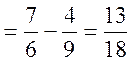
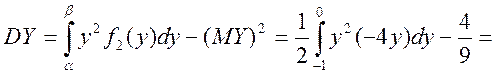
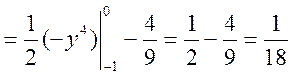
![]() — умовне математичне сподівання складової
— умовне математичне сподівання складової ![]() при умові
при умові ![]() є
число, яке визначається формулою
є
число, яке визначається формулою
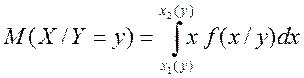 ,
,
де ![]() — числа.
— числа.
Отже
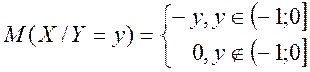
![]()
![]() — умовне математичне сподівання складової
— умовне математичне сподівання складової ![]() при умові
при умові ![]() є
число, яке визначається формулою
є
число, яке визначається формулою
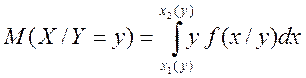 ,
,
де ![]() — числа.
— числа.
Отже
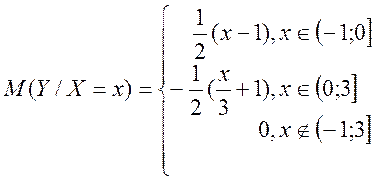
![]()
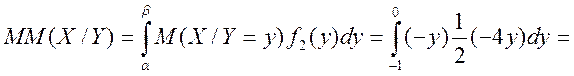
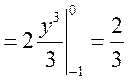
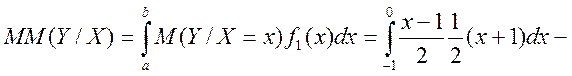
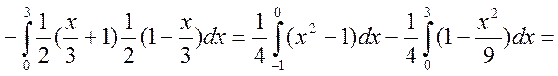
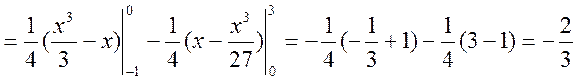
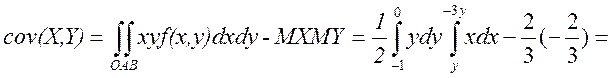
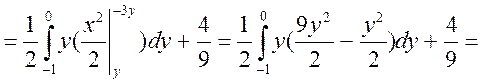
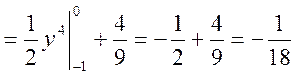
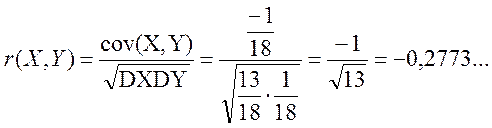
в) випишемо коваріаційну матрицю
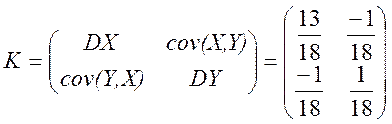
Випадкові
величини ![]() залежні, оскільки, наприклад,
залежні, оскільки, наприклад,
![]()
і корельовані, оскільки
![]() .
.
Відповідь:
розподіли ![]()
![]()
![]()
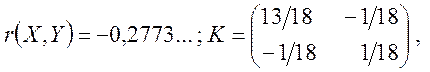 X,Y — залежні, корельовано.
X,Y — залежні, корельовано.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.