Министерство образования и науки Украини
Сумський государственный университет
Кафедра прикладной математики
Курсовая работа
по курсу
“Численные методы”
по теме
Виполнил: студент групи ПМ-81
Русаков С.Л.
Проверил : доц. Назаренко Л. Д.
Суми 2001
В реальной жизни различные задачи в области экономики, биологии, физики подчиняются определенным законам. Однако на систему могут оказывать влияние случайные факторы, и в большинстве случаев необходимо оценить это влияние.
Метод Монте-Карло позволяет моделировать любой процесс, на протекание которого оказывают влияние случайные факторы. Для многих математических задач, не связанных с какими-либо случайностями можно искусственно придумать вероятностную модель, позволяющую решать эти задачи.
В вероятностных задачах, очевидно, необходимо определять вероятностные характеристики случайных величин – математическое ожидание и дисперсию. В работе рассмотрен пример моделирования системы массового обслуживания.
Понятие мат. ожидания тесно связано с понятием опред. интеграла. Если случ. фактор зависит от нескольких параметров, т.е. он многомерный, то решается задача о вычислении кратных интегралов.
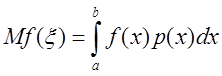
1. Общая схема метода Монте-Карло
По известным формулам теории вероятности
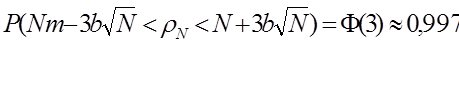
Преобразовав его, получим
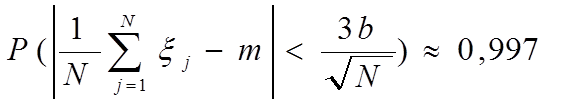
отсюда следует, что при больших n
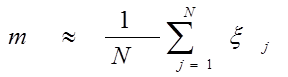
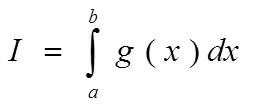
выбираем произвольную плотность распределения p(x), определенную на (a,b). Выберем случайную величину
![]()
Тогда
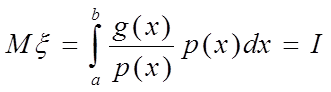
Рассмотрим N независимых случайных величин ![]() и применим к их сумме центральную
предельную теорему
и применим к их сумме центральную
предельную теорему
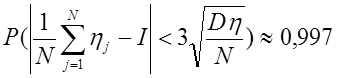
При больших N имеем оценку
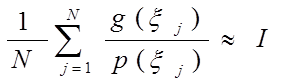
далее задаемся N, выбираем N случайных величин и по последней формуле вычисляем значение интеграла.
3. Вычисление кратных интегралов методом Монте-Карло
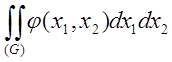
Интеграл
численно равен объему 2-мерного цилиндроида, на основании G и ограниченным
сверху поверхностью ![]()
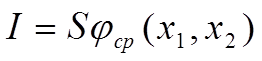
Пусть aj , Aj соответственно нижние и верхние пределы интегрирования.
Возьмем область интегрирования внутри 2-мерного параллепипеда со сторонами (A1-a1)(A2-a2). Возьмем внутри N случайных точек, тогда
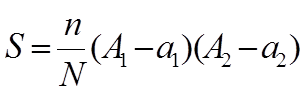
для тех точек, которые попали в область интегрирования
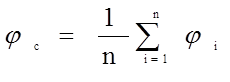
Искомый интеграл равен
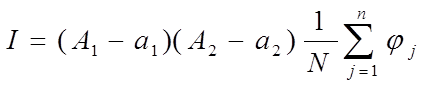
Алгоритм расчета:
1) выбираем число испытаний
2) вычисляем по
формуле x[j] = a[j] + (A[j]-a[j])*![]() - точки разбиения
- точки разбиения
3) вычисляем значение I
3. Система массового обслуживания
Имеется n линий, каждая из которых может обслуживать заявки за время tz. Момент поступления заявки – случайная величина. Если линия занята, то заявка передается свободной линии, в случае, если заняты все линии, система выдает отказ. Необходимо в среднем определить, сколько заявок обслужит система за время Т.
В работе разыгрывается время поступления следующей заявки в соответствии с методом Монте-Карло и моделируется процесс работы системы. Испытание повторяется N раз и затем результаты усредняются.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.