Сумской государственный университет
Кафедра прикладной математики
по дисциплине ”Численные методы” на тему:
” Приближенное интегрирование дифференциальных уравнений”
Выполнила студентка III курса
группы ПМ-92
Максименко О.В.
Преподаватель Назаренко Л.Д.
Сумы 2002
1. Введение.
2. Постановка задачи
3. Приближенное интегрирование дифференциальных уравнений, основанное на интерполяции. Формулы Адамса
3.1. Формула Адамса с первыми разностями
3.2. Формула Адамса со вторыми разностями
4. Методы составления начала таблицы для применения формул Адамса
4.1. Метод Эйлера с уравниванием
4.2. Метод последовательных приближений А. Н. Крылова
4.3. Метод Адамса-Крылова
5. О точности методов численного интегрирования дифференциальных уравнений. Контроль
6. Алгоритмы используемых методов
7. Результаты. Выводы
Многие технические задачи приводят к необходимости отыскания решения дифференциального уравнения, удовлетворяющего тем или иным начальным условиям. Как известно, дифференциальные уравнения удается проинтегрировать в конечном виде лишь в отдельных специальных случаях, да и то при этом часто получаются выражения, определяющие искомую функцию в неявной форме, пользование которыми весьма затруднительно. Поэтому в инженерной практике приходится прибегать к приближенному интегрированию дифференциальных уравнений.
Рассмотрим дифференциальное уравнение первого порядка, разрешенное относительно производной:
![]() (1)
(1)
Найти приближенное численное решение дифференциального уравнения, это значит составить таблицу приближенных значений интеграла дифференциального уравнения, удовлетворяющего заданным начальным условиям. Пусть y(x) – решение уравнения (1) и х=х0 – начальное значение аргумента. Начальное условие для решения уравнения (1) задается в виде
y(x0)=y0, (2)
где y0 – заданное число.
Очевидно, что ставить вопрос об отыскании приближенных
значений интеграла y(x)
уравнения (1) можно в том и только в том случае, если решение y(x), удовлетворяющее
условию (2), существует и единственно. Как известно из общей теории
дифференциальных уравнений, для этого достаточно, чтобы фигурирующая в правой
части уравнения (1) функция f(x,y) была непрерывна в
рассматриваемой области по обоим аргументам и имела ограниченную частную
производную 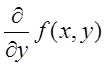 .
.
Идея метода Адамса заключается в том, что производная на соответствующем участке заменяется полиномом первой, второй или более высокой степени, а сам интеграл, следовательно, заменяется полиномом степени на еденицу выше.
Для получения рабочих формул воспользуемся интерполяционной формулой Ньютона для интерполирования назад:
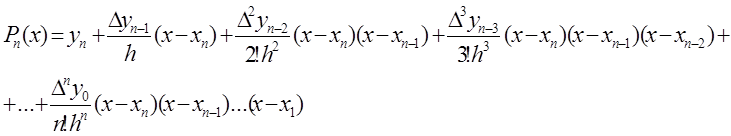 (3)
(3)
Пусть выбрано число h – шаг таблицы, и промежуток интегрирования точками x1=x0+h, x2=x1+h, … разбивается на участки равной длины.
На участке [x0,x2] изменения независимой переменной заменим
производную ![]() искомого интеграла интерполяционным
полиномом Ньютона (для интерполирования назад) первой степени.
искомого интеграла интерполяционным
полиномом Ньютона (для интерполирования назад) первой степени.
По формуле (3) получим
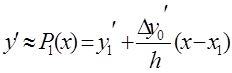 (4)
(4)
Обозначим в дальнейшем для уравнения(1)
![]() (k=0,1,2,…) (5)
(k=0,1,2,…) (5)
Тогда для любой разности
![]() (6)
(6)
и формула (4) примет вид
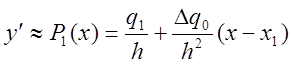 .
.
Интегрируя теперь по промежутку [x1,x2] и имея в виду, что x2-x1=h, получим
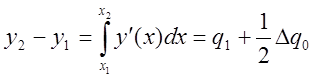 .
.
Отсюда
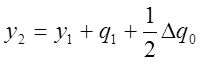 .
.
Аналогично, применяя те же рассуждения к участку [x1,x3], получим
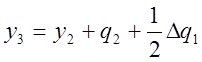 , и
т.д.
, и
т.д.
Отсюда в общем случае
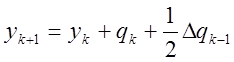 (k=1,2,…)(7)
(k=1,2,…)(7)
На участке [x0,x3] изменения независимой переменной заменим
производную ![]() искомого интеграла интерполяционным
полиномом Ньютона второй степени. По формуле (3) получим
искомого интеграла интерполяционным
полиномом Ньютона второй степени. По формуле (3) получим
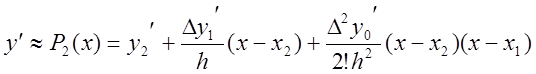
Отсюда в силу (5) и (6)
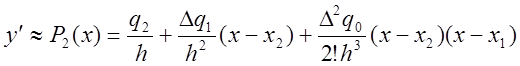 .
.
Преобразуем
последнее слагаемое. Так как ![]()
![]() .
.
Отсюда
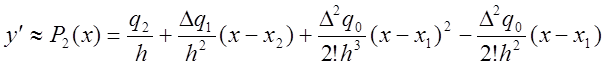 .
.
Интегрируя теперь по промежутку [x2,x3] и имея в виду, что ![]() ,
,
![]() , получим
, получим
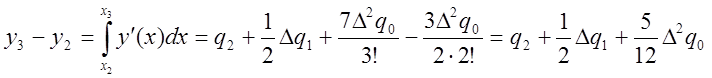 .
.
Отсюда
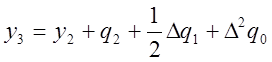 .
.
Аналогично, применяя те же рассуждения к участку [x1,x4], получим
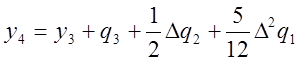 , и т.д.
, и т.д.
Отсюда в общем случае
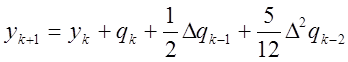 (k=2,3,…)(8)
(k=2,3,…)(8)
Точно так же можно получить формулы Адамса с третьими и более высокими разностями. Например:
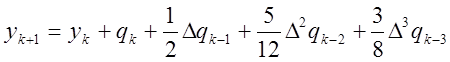 (k=3,4,…), (9)
(k=3,4,…), (9)
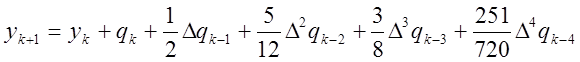 (k=4,5,…). (10)
(k=4,5,…). (10)
Эти формулы позволяют при том же шаге получить более точные результаты, чем формулы (7) или (8), однако при этом повышается и сложность расчетов. В дальнейшем в качестве основной мы выберем формулу (8).
Для начала вычисления по формулам Адамса необходимо знать значения искомого интеграла дифференциального уравнения не в одной, а в нескольких точках: при применении формулы с первыми разностями (7) – в точках x0 и x1=x0+h; при применении формулы со вторыми разностями (8) – в точках x0, x1=x0+h и x2=x0+2h. Для вычисления этих первых значений интеграла существует много различных методов. Ниже будут изложены некоторые из них. Изложение будем вести применительно к формуле (8), требующей предварительного вычисления значений искомого интеграла дифференциального уравнения в двух точках (значение интеграла в точке х0 задается начальным условием).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.