Приближенное интегрирование дифференциальных уравнений, страница 2

Метод Эйлера с уравниванием

Этот метод может давать очень хорошие результаты при сравнительно несложной вычислительной схеме. Порядок погрешности на каждом шаге таков же, как у формулы (8).

Следует напомнить в чем состоит сам метод Эйлера.

А состоит этот простейший метод приближенного интегрирования дифференциальных уравнений в том, что на малом промежутке изменения независимой переменной  интегральная кривая   заменяется отрезком прямой (касательной)  _. Отсюда  и процесс можно повторить для промежутка  и т.д. Число h является здесь шагом таблицы. Рабочая формула для определения значений у по методу Эйлера имеет вид

,   (11)

где .

Вычисления по этому методу очень просты, но при значительном изменении независимой переменной  приближенные значения интеграла дифференциального уравнения могут сильно отличаться от точных значений, так как, вообще говоря, погрешность накапливается с каждым шагом.

Значительно лучшие результаты можно получить, несколько усовершенствовав метод Эйлера.

Обозначим . Тогда  и формулу (11) перепишем так:

   (12)

Усовершенствование метода Эйлера (уравнивание) заключается в том, что вычисленное по формуле (12) (или, что одно и то же, по формуле (11)) значение  уточняется по следующей схеме.

Обозначим найденное значение через  и вычислим . Заменим теперь в формуле (12)  средним арифметическим значений производных в граничных точках 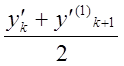 и определим  .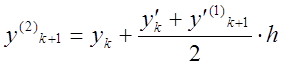         

Найденное значение  позволяет вычислить и, аналогично предыдущему, определить

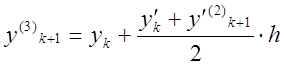 и т.д.

Этот процесс продолжается до тех пор, пока в пределах заданной точности не совпадут результаты двух последовательных вычислений значений . После этого тем же методом вычисляется  и т.д.

Метод последовательных приближений А. Н. Крылова.         Метод Адамса-Крылова

В дальнейшем основным будем считать метод составления начала таблицы путем последовательных приближений, указанный акад. А. Н. Крыловым.

В основе вычислений по этому методу лежит формула

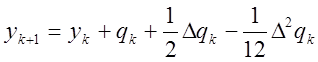,       (13)

правая часть которой, в отличие от формулы (8), содержит разности с одним и тем же нижним индексом. Формула (13),подобно тому, как формула (8) была получена из формулы Ньютона для интерполирования назад, получается из формулы Ньютона для интерполирования вперед:

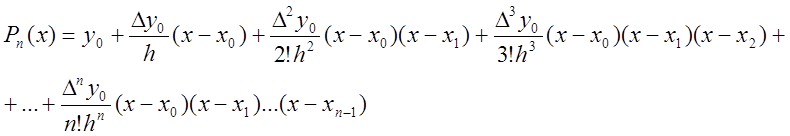
Полагая в (13) k=0, получим

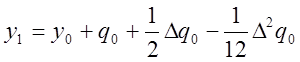.          (14)

При k=1 из (13) следует   

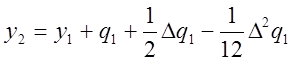 .  Но  , и считая, наконец, что вторые разности остаются практически постоянными, положим  .

Тогда

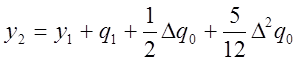.                 (15)

Формулы (14)-(15), называемые формулами Крылова, дают возможность построить начало таблицы для формулы Адамса (8). Эти формулы получены при условии практического постоянства вторых разностей, но это же условие лежит в основе применимости и самой формулы (8) (разности порядка выше второго практически равны нулю).

Фигурирующие в формулах (14)-(15) разности  и  требуют для вычисления предварительного знания значений . Это обстоятельство не дает возможности воспользоваться сразу указанными формулами. Однако можно вводить эти формулы в действие постепенно, удерживая в них лишь те члены, которые в данный момент можно вычислить. Полученные таким образом значения   можно рассматривать как некоторые приближения и с их помощью вычислить пока приближенные значения для соответствующих разностей. Вводя вычисленные таким способом разности в формулы (14)-(15), получаем возможность найти более точные  значения для  и т.д. Этот метод последовательного уточнения вычисляемых значений называется методом последовательных приближений.

Покажем, как строятся соответствующие приближения. Дополнительные вычисления проводятся во вспомогательной таблице.

Зная из начального условия значения , при выбранном шаге h находим в силу данного уравнения    . Таким образом, в начале вычисления вспомогательная таблица примет вид :

k
0